0.7
Пошаговое объяснение:
всего в коробке 7+3=10 шаров
вероятность вынуть первый белый шар равна 7/10
вероятность вынуть первый черный шар равна 3/10
А теперь смотрим, если первым вытянули белый шар, то в коробке осталось 6 белых шаров из 9 оставшихся, тогда второй белый шар будет вынут с вероятностью 6/9=2/3.
Если первым вытянули черный шар, то в коробке осталось 7 белых шаров из 9 оставшихся, тогда второй белый шар будет вынут с вероятностью 7/9
Задача на полную вероятность:
Гипотезы:
B - первым вынули белый шар.
C - первым вынули черный шар.
P(B)=7/10
P(C)=3/10
A-вторым вынули белый шар.
Условные вероятности:
A/B - вторым вынули белый шар, при условии что первым вынули белый шар.
A/C-вторым вынули белый шар, при условии что первым вынули черный шар.
P(A/B)=2/3
P(A/C)=7/9
Формула полной вероятности:
P(A)=P(B)*P(A/B)+P(C)*P(A/C)
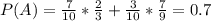
0.7
Пошаговое объяснение:
всего в коробке 7+3=10 шаров
вероятность вынуть первый белый шар равна 7/10
вероятность вынуть первый черный шар равна 3/10
А теперь смотрим, если первым вытянули белый шар, то в коробке осталось 6 белых шаров из 9 оставшихся, тогда второй белый шар будет вынут с вероятностью 6/9=2/3.
Если первым вытянули черный шар, то в коробке осталось 7 белых шаров из 9 оставшихся, тогда второй белый шар будет вынут с вероятностью 7/9
Задача на полную вероятность:
Гипотезы:
B - первым вынули белый шар.
C - первым вынули черный шар.
P(B)=7/10
P(C)=3/10
A-вторым вынули белый шар.
Условные вероятности:
A/B - вторым вынули белый шар, при условии что первым вынули белый шар.
A/C-вторым вынули белый шар, при условии что первым вынули черный шар.
P(A/B)=2/3
P(A/C)=7/9
Формула полной вероятности:
P(A)=P(B)*P(A/B)+P(C)*P(A/C)
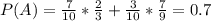
березы = 1/5 часть
клены = 1/3 часть
дубы = 1/3 часть + 18
липы = 94
94+18 = 112 - известная часть деревьев(липы и часть дубов)
1 -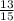 =
= 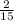 - известная часть деревьев(112 шт)
- известная часть деревьев(112 шт)
Составим пропорцию:
1(целое) - x
x = 112 * :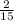 =
=
112*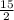 = 840 деревьев
= 840 деревьев
тогда:
берез - 168
кленов - 280
дубов - 280 + 18 = 298
лип = 94
Итого 168+280+298+94 = 840 деревьев