х км/ч - собственная скорость парохода
у км/ч - скорость течения ( скорость плота)
1 - путь в одну сторону
(х+у) км/ч - скорость парохода по течению
(х-у) км/ч - скорость парохода против течения
t=S:v
1/(х+у)=6
х+у=1/6 (пути/час) - скорость парох. по течению
1/(х-у)=10
(х-у)=1/10 (пути/час) - скорость парох. против течения
Vтеч.=(V по теч. - V прот. теч) :2
V теч=(1/6 - 1/10) : 2=1/30(пути/час) - скорость плота по течению(против теч. он не плывет)
1 : 1/30 = 30(час) - время, за кот. плот проплывет расстояние между пристанями.
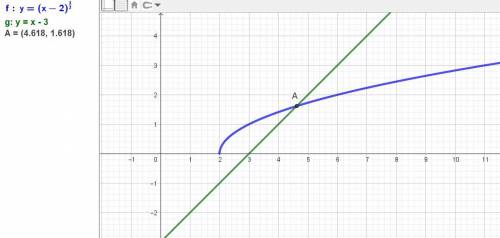
Дано уравнение: √(x - 2) = x - 3.
ОДЗ: х - 2 > 0, x > 2.
Надо обе части уравнения возвести в квадрат.
х - 2 = х² - 6х + 9.
Получаем квадратное уравнение:
х² - 7x + 11 = 0.
Квадратное уравнение, решаем относительно x:
Ищем дискриминант:
D=(-7)^2-4*1*11=49-4*11=49-44=5;
Дискриминант больше 0, уравнение имеет 2 корня:
x_1=(√5-(-7))/(2*1)=(√5+7)/2=√5/2+7/2=√5/2+3.5~~4.618034;
x_2=(-√5-(-7))/(2*1)=(-√5+7)/2=-√5/2+7/2=-√5/2+3.5~~2.381966.
Получили 2 корня - это результат лишнего корня при возведении в квадрат, но должна быть одна точка пересечения одной ветви параболы и прямой.
Второй корень не подходит.
ответ: х1 = √5/2+3,5.