Если для любого 
из области определения функции выполняется равенство 
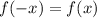, то функция является чётной.
Если для любого из области определения функции выполняется равенство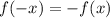 
, то данная функция является нечётной.
Если же ни одно из этих равенств не выполняется, то функция не является ни чётной, ни нечётной.
б)
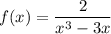
Отсюда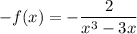 
.
Для начала найдём область определения данной функции. Её знаменатель не должен быть равен нулю:
Итак, область определения нашли. Теперь найдём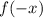 
, для этого все в функции заменим на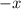 
.
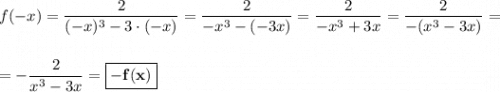
Таким образом, данная функция является нечётной.
в)
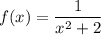
Отсюда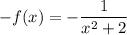 
.
Для начала найдём область определения данной функции. Её знаменатель не должен быть равен нулю:
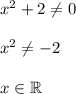
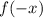То есть, для данной функции за можно принять любое действительное число. Теперь найдём , для этого все в функции заменим на .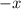
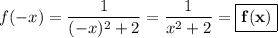
Таким образом, данная функция является чётной.
г)
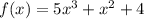
Отсюда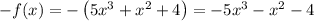 
.
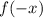может быть любым числом, поскольку никаких ограничений на аргумент здесь не накладывается. Теперь найдём , для этого все в функции заменим на .
.
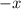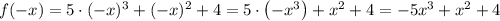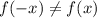и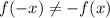 
, а значит, функция не является ни чётной, ни нечётной.
Пошаго
1. В таблице 1 даны характеристики звезд: температура Т в К, светимость, выраженная в светимостях Солнца (светимость Солнца принята за 1).
2. Постройте диаграмму Герцшпрунга - Рессела для приведенных в таблице звезд (звезды подписать). По вертикальной оси откладывайте светимость (в светимостях Солнца), по горизонтальной – температуру (рис.3). Горизонтальная шкала неравномерна.
3. Нанесите на диаграмму пунктиром главную последовательность.
4. Используя таблицу «Спектральная классификация звезд» (рис.1), постройте на диаграмме вертикальные цветные полосы, соответствующие цвету звезд (рис.1,2).
5. Отметьте на диаграмме области, где расположены красные гиганты, белые карлики, сверхгиганты.
6. Построение выполнять на рис.3 (перенесите в тетрадь).вое объяснение:
2)0,68*1,5=1,02
3)61,71:1,02=60,5
4)63,163:7,61=8,3
5)60,5+8,3=68,8