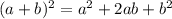упрощаем выражение в квадрате: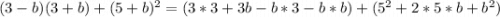
Теперь просто открываем скобки и приводим общие члены:
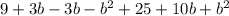- можем сократить одинаковые члены с разными знаками, например 
и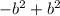 
сокращаем, потому что результат вычислений этих выражений равен 0.
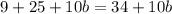- результат.
=================================
2. 
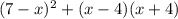
Точно также как и в первом примере, сперва первое выражение в квадрате упрощаем с формулы квадрата суммы, два вторых выражения переумножаем:
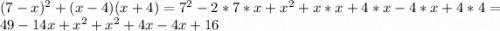
Теперь приводим общие члены, с разными знаками - "уничтожаем":
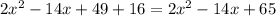
1. Является ли неравенство 2x >5 строгим?
а) да
2 Можно ли почленно складывать верные неравенства одного знака?
а) да
3. Существует ли целое число , принадлежащее промежутку
[-3,9; -3,27]
в) нет
4. X≥ 3. ответ. (3; +∞). Верно ли записан геометрический промежуток?
б) нет
5. Является и число 17 наибольшим целым числом числового промежутка (-9; 18)?
а) да
6. Верно ли, что 7х - 5 <0, если x>2?
б) нет
7. Верно ли, что если а<в, то а- в= 0?
б) нет
Припишем в конце нули к этим дробям:
14,5 = 14,50
14,6 = 14,60
Между 50-сотых и 60-сотых можно написать любые числа от 1 до 9, чтобы дробь была заключена между данными числами:
14,51; 14,52; 14,53; 14,54; 14,55; 14,56; 14,57; 14,58; 14,59 - любая из этих дробей.
Или можно приписать 2 нуля в конце: 14,500 и 14,600. Тогда вариантов ещё больше:
14,511; 14,537; 14,789 и т.д...