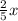, следовательно, во второй день 
, а в третий день - оставшиеся 90 км согласно этим данным составим и решим уравнение:
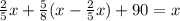
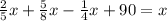
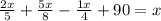/·40
умножаем на 40 для того, чтобы избавиться от знаменателей
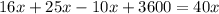
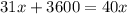
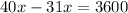
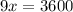
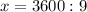
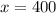(км) - весь путь.
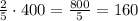(км) - проплыл ледокол в первый день.
400-(160+90)=400-250=150 (км) - проплыл ледокол во второй день Примем за 1 целое – путь пройденный ледоколом за 3 дня, тогда
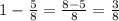(часть) - путь пройденный в третий день.
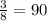км
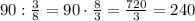(км) - пройденный путь за второй и третий день вместе.
240-90=150 (км) - проплыл ледокол во второй день.
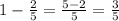(часть) - оставшийся путь после первого дня.
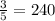км
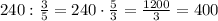(км) - весь путь.
400-240=160 (км) - проплыл ледокол в первый день Предположим, что х – это весь путь пройденный ледоколом, тогда в первый день он проплыл 0,4x, следовательно, во второй день 0,625(x-0,4x) или 0,375х, а в третий день - оставшиеся 90 км
согласно этим данным составим и решим уравнение:
0,4х+0,375х+90=х
0,775х+90=х
х-0,775х=90
0,225х=90
х=90:0,225
х=400 (км) - весь путь.
0,4х=0,4·400=160 (км) - проплыл ледокол в первый день.
0,375х=0,375·400=150 (км) - проплыл ледокол во второй день.
ответ: в первый день ледокол проплыл 160 км, а во второй - 150 км.
на 20% площадь прямоугольника меньше площади квадрата
Пошаговое объяснение:
Р квадрата = 4а = 6 м
а = Р/4 = 6/4 = 1,5 м - длина стороны квадрата
S квадрата = a² = 1,5² = 2,25 м²
20% = 20/100 = 0,2
Р прям-ка = 6 + 6*0,2 = 6 + 1,2 = 7,2 (см)
х м ширина прям-ка, тогда длина = 5х м
Р прям-ка = 2(а + b)
2(5х+х) = 7,2
12х = 7,2
х = 7,2/12
х = 0,6 (м) - ширина прям-ка
0,6*5 = 3 (м) - длина прям-ка
S прям-ка = a*b = 0,6 * 3 = 1,8 м²
2,25 м² - 100%
1,8 м² - х%
х = 1,8*100/2,5 = 80% составляет S прям-ка
100% - 80% = 20% - на 20% площадь прямоугольника меньше площади квадрата
18
Пошаговое объяснение:
Неравенство:
9x^2 - x + 1/36 ≥ -9y^2 + y - axy
Условие: |x| = |y|, то есть или y = -x, или y = x.
Умножим все на 36 (избавимся от дробей) и перенесем все налево:
324x^2 - 36x + 1 + 324y^2 - 36y + 36axy ≥ 0
324(x^2 + y^2) - 36(x + y) + 36axy + 1 ≥ 0
1) Применим первое из условий: y = -x.
Тогда x^2 + y^2 = 2x^2; x + y = 0; 36axy = -36ax^2:
324*2x^2 - 0 - 36ax^2 + 1 ≥ 0
(648 - 36a)*x^2 + 1 ≥ 0
Чтобы это было верно при любом х, это должна быть сумма двух неотрицательных чисел. Значит:
648 - 36a ≥ 0
36a ≤ 648
a ≤ 18
2) Применим второе из условий: y = x.
Тогда x^2 + y^2 = 2x^2; x + y = 2x; 36axy = 36ax^2:
324*2x^2 - 36*2x + 36ax^2 + 1 ≥ 0
(648 + 36a)x^2 - 72x + 1 ≥ 0
Чтобы это было верно при любом х, выражение слева не должно иметь корней.
D = (-72)^2 - 4*1(648 + 36a) ≤ 0
5184 - 2592 - 144a ≤ 0
2592 - 144a ≤ 0
144a ≥ 2592
a ≥ 18
При a ≤ 18 есть решение, что подходят любые х и у, если y = -x.
А при а ≥ 18 есть решение, что подходят любые x и y, если y = x.
Таким образом, решение есть при любом а.
Но возможно, что по мнению авторов задачи, правильный ответ: 18.
1)1-2/5=3/5 пути -осталось.
2)3/5*5/8=3/8 пути во второй день.
3)3/5-3/8=9/40 пути в третий день.
4) 90*40:9=400км-весь путь.
5)400*2:5=160км в первый день.
6)400*3:8=150км во второй день.