В партии всего 10 - 4 = 6 хороших деталей.
1) Найдем вероятность того, что среди выбранных 3 деталей нет дефектных.
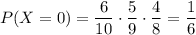
2) Найдем вероятность того, что среди выбранных 3 деталей одна дефектная.
Общее число возможных элементарных исходов равно числу которыми можно извлечь 3 детали из 10: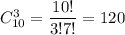 
Выбрать две хороших деталей можно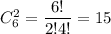 
а одну дефектную деталь - 
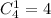По правилу произведения, всего 
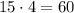число благоприятных исходов.
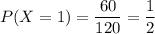
3) Найдем вероятность того, что среди выбранных 3 деталей 2 дефектных.
Выбрать одну хорошую деталь можно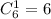 
а две дефектных - 
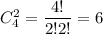Всего таких
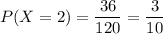
4) Найдем вероятность того, что все выбранные детали дефектные.
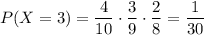
Закон распределения случайной величины:
Xi 0 1 2 3
Pi 1/6 1/2 3/10 1/30
(Запишите это именно в виде таблицы).
Математическое ожидание случайной величины X:
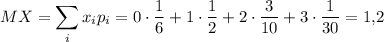
Х²+12ху=64-36
Х=6+6у
(6+6у)²+12у*(6+6у)=28
(36+72у+36у²)+72у+72у²=28
36у²+72у²+2×72у+36-28=0
108у²+144у+8=0
27у²+36у+2=0
Дискриминант: 36²-4×2×27=1296-216=1080
Корень из дискриминанта = 6корень30
У1=(-36-6корень30) /2×27 = -6(6+корень30) / 2×27 = (-6-корень30) / 9
У2= (-36+6корень30)/2×27 = 6(-6+корень30)/2×27 = (корень30 - 6)/9
Если у1= (-6-корень30)/9, то х1= 6 + 6×(-6-корень30)/9 = 6+ (-12-2корень30)/3 = (18-12-2корень30)/3 = (6-2корень30)/3 = 2/3 × (3-корень30)
Если у2=(корень30 - 6)/9, то х2= 6+ (2*(корень30-6))/3 = (18-12+2корень30)/3 = (6+2корень30)/3 = 2/3 × (3+корень30)
у=-3х-6 параллелен у=-3х+6, поскольку при иксике у них минус тройки.