Пусть основание меньшей стороны равнобедренной трапеции равно a, а большей – b. Тогда её площадь можно вычислить по формуле:
S = (a + b) * h / 2,
где h – высота трапеции.
Для нашей трапеции справедливы следующие соотношения:
a = 32 см, b = 50 см, α = 45°.
Так как трапеция равнобедренная, то её высота h может быть найдена по формуле:
h = a * tg(α/2) = 32 * tg(45°/2) ≈ 15,45 см.
Теперь можем вычислить площадь трапеции:
S = (a + b) * h / 2 = (32 + 50) * 15,45 / 2 ≈ 709,8 см².
ответ: площадь трапеции равна примерно 709,8 квадратных сантиметров.
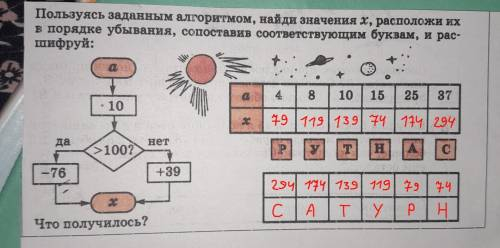
ответ: сатурн
Пошаговое объяснение:
Используя приведенный алгоритм, найдем все значения x через a:
a = 4: 4 * 10 = 40; 40 > 100 - нет => x = 40 + 39 = 79 (Р)
a = 8: 8 * 10 = 80; 80 > 100 - нет => x = 80 + 39 = 119 (У)
a = 10: 10 * 10 = 100; 100 > 100 - нет => x = 100 + 39 = 139 (Т)
a = 15; 15 * 10 = 150; 150 > 100 - да => x = 150 - 76 = 74 (Н)
a = 25; 25 * 10 = 250; 250 > 100 - да => x = 250 - 76 = 174 (А)
a = 37; 37 * 10 = 370; 370 > 100 - да => x = 370 - 76 = 294 (С)
Расположим все x по убыванию:
294; 174; 139; 119; 79; 74
Заполним таблицу и получим слово: сатурн
3/5 - 1/10 =6/10-1/10=5/10=0,5
1/12 + 5/6 =1/12+10/12=11/12
1/3 + 1/4 =4/12+3/12=7/12
1/3 + 2/5 =5/15+6/15=11/15
1/2 - 1/4 =2/4-1/4=1/4=0,25
8/7 - 1 =8/7-7/7=1/7
1/4 - 1/5 =5/20-4/20=1/20=0,05
1/2 + 3/7 =7/14+6/14=13/14
3/4 - 1/8 =12/16-2/16=11/16
1/5 + 1/6 =6/30+5/30=11/30
4/15 + 2/5 =4/15+6/15=10/15=2/3
7/10 - 1/2 =7/10-5/10=2/10=0,2
1/3 - 1/4 =4/12-3/12=1/12