Определенным интегралом функции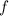 
на отрезке ![[a;b]](/tpl/images/1357/5478/a6d4a.png)
называют предел, когда он существует, её интегральной суммы при λ (Т) =>0, который обозначают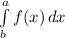 
Геометрический смысл определенного интеграла:
Криволинейная трапеция – это фигура, ограниченная сверху кривой y=f(x), снизу – отрезком [a;b], слева – прямой х = а, справа – прямой х = b.
Определенный интеграл – площадь криволинейной трапеции
Достаточное условие существование определенного интеграла: если функция y=f(x) непрерывна на [a;b], то она интегрируема на этом отрезке.
Обязательная составляющая криволинейной трапеции – нижнее основание в виде [a;b] и верхняя часть в виде кривой y=f(x).
80
Пошаговое объяснение:
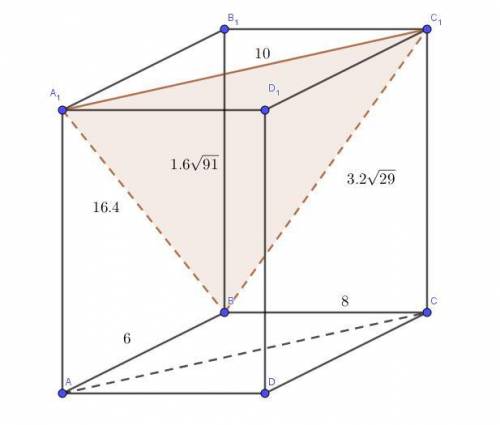
Найдем данное сечение:
Соединим точки BA₁, так как сечение проходит через прямую BA₁.
По условию, наше сечение параллельно АС, значит в этой плоскости должна найтись такая прямая, которая будет параллельна АС.
Для этого проведем отрезок из точки A₁ до С₁, ведь А₁С₁║AC.
Соединим точки В и С₁, так как они лежат в одной плоскости ВВ₁С₁.
ΔА₁ВС₁ - искомое сечение.
Все 3 измерения нашего параллелепипеда известны, поэтому находим стороны треугольника по теореме Пифагора:
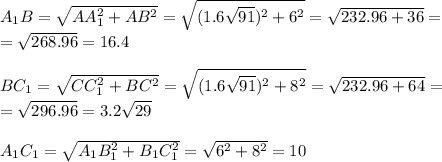
Площадь искомого треугольника найдем по формуле Герона:
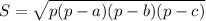
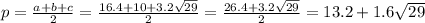
2120
12500
5060 десятая часть