Решить уровнение 3x²+6x=0 9y²-4=0 3x²-2x-1=0

👇

Увидеть ответ

Ответ:

guarginia666

30.11.2021

Решить уровнение 3x²+6x=0 9y²-4=0 3x²-2x-1=0

4,6(54 оценок)

Ответ:

dashusha0703

30.11.2021

3х^2+6х=0
3х*(х+2)=0
х*(х+2)=0
х=0
х+2=0
ответ:
х1=0
х2=-2

9у^2-4=0
9у^2=4
ответ:
у1=2/3
у2=-2/3

3х^2-2х-1=0
3х^2+х-3х-1=0
х*(3х+1)-(3х+1)=0
(3х+1):(х-1)=0
3х+1=0
х-1=0
ответ:
х1=-1/3
х2=1

4,7(15 оценок)

Открыть все ответы

Ответ:

bayosoz5oe5

30.11.2021

Пошаговое объяснение:

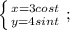
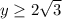
$\left \{ {{x=3cost} \atop {y=4sint}} \right. ;$ $y\geq 2\sqrt{3}$

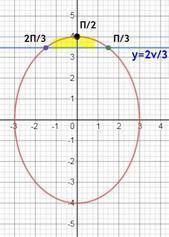
для простоты рисования графика, отмечу, что мы фактически имеем эллипс

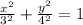
$\frac{x^2}{3^2} +\frac{y^2}{4^2} =1$

вот рисуем этот эллипс и прямую у = 2√3. в осях ох оу мы нарисовали график и видим все границы по х и у

теперь нам надо перейти к пределам интегрирования по t

у = 2√3 = 4sin t ⇒ t₁ = π/3; t₂= 2π/3

однако, мы видим, что нужная нам фигура состоит из двух симметричных относительно оси оу фигур. найдем площадь одной и умножим потом на 2

надл найти "высшую" точку эллипса. это будет точка при х = 0

х = 0 = 3cost ⇒ t = π/2

вот и все, теперь считаем интергал

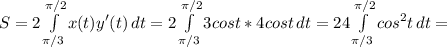
$S=2\int\limits^{\pi /2}_{\pi /3} {x(t)y'(t)} \, dt =2\int\limits^{\pi /2}_{\pi /3} {3cost*4cost} \, dt=24\int\limits^{\pi /2}_{\pi /3} {cos^2t}\,dt=$

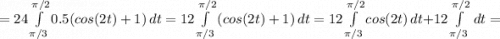
$=24\int\limits^{\pi /2}_{\pi /3} {0.5(cos(2t)+1)} \, dt =12\int\limits^{\pi /2}_{\pi /3} {(cos(2t)+1)} \, dt =12\int\limits^{\pi /2}_{\pi /3} {cos(2t)} \, dt +12\int\limits^{\pi /2}_{\pi /3} {} \, dt =$

теперь для первого интеграла мы сделаем замену u=2t; du=2dt, тогда в этом интеграле поменяются пределы интегрирования

верхний станет π, а нижний 2π/3, и вот

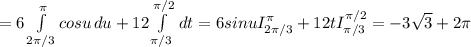
$=6\int\limits^\pi _{2\pi /3} {cosu} \, du+12\int\limits^{\pi /2}_{\pi /3} {} \, dt=6sinuI_{2\pi /3} ^\pi +12tI_{\pi /3}^{\pi /2}= -3\sqrt{3} +2\pi$

Вычислите площадь фигуры, ограниченной заданными линиями {x = 3 cos t, y = 4 sin t, y >= 2√3.

4,4(22 оценок)

Ответ:

Убийца967

30.11.2021

Соотношение градусов и радиан : 180° = π радиан

Формула для перевода градусной меры в радианную

\dfrac {\alpha\textdegree\cdot \pi}{180\textdegree}=\alpha

180\textdegree

α\textdegree⋅π

=α радиан

\begin{gathered}60\textdegree=\dfrac{60\textdegree\cdot \pi}{180\textdegree}=\dfrac{\pi}3120\textdegree=\dfrac{120\textdegree\cdot \pi}{180\textdegree}=\dfrac{2\pi}3150\textdegree=\dfrac{150\textdegree\cdot \pi}{180\textdegree}=\dfrac{5\pi}6\end{gathered}

60\textdegree=

180\textdegree

60\textdegree⋅π

120\textdegree=

180\textdegree

120\textdegree⋅π

2π

150\textdegree=

180\textdegree

150\textdegree⋅π

5π

\begin{gathered}225\textdegree=\dfrac{225\textdegree\cdot \pi}{180\textdegree}=\dfrac{5\pi}4240\textdegree=\dfrac{240\textdegree\cdot \pi}{180\textdegree}=\dfrac{4\pi}3300\textdegree=\dfrac{300\textdegree\cdot \pi}{180\textdegree}=\dfrac{5\pi}3345\textdegree=\dfrac{345\textdegree\cdot \pi}{180\textdegree}=\dfrac{23\pi}{12}\end{gathered}

225\textdegree=

180\textdegree

225\textdegree⋅π

5π

240\textdegree=

180\textdegree

240\textdegree⋅π

4π

300\textdegree=

180\textdegree

300\textdegree⋅π

5π