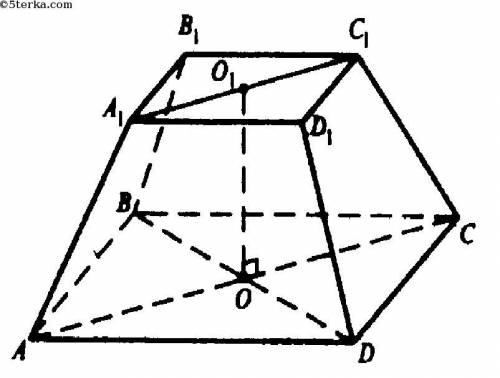
Пусть дана правильная четырехугольная усеченная пирамида 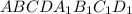 , где
, где 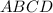 и
и 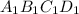 — квадраты со сторонами соответственно 22 см и 6 см. Боковое ребро пирамиды
— квадраты со сторонами соответственно 22 см и 6 см. Боковое ребро пирамиды 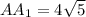 см.
см.
Найдем площадь 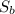 боковой поверхности заданной пирамиды.
боковой поверхности заданной пирамиды.
Для того чтобы ее найти, следует найти площадь одной боковой грани (равнобедренной трапеции) и ее умножить на 4.
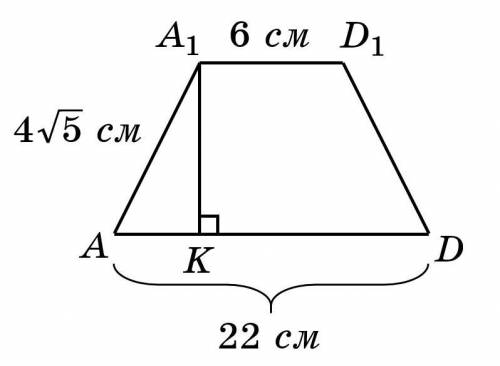
Рассмотрим равнобедренную трапецию 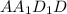
Проведем в трапеции высоту 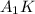
Найдем 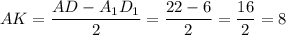 см
см
Рассмотрим прямоугольный треугольник 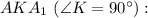
По теореме Пифагора: 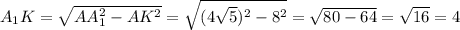 см.
см.
Следовательно, площадь трапеции равна
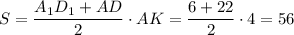 см².
см².
Таким образом, 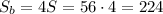 см².
см².
ответ: 224 см².
S1=2*Пи*R
S1=2*3,14*20=125,6 см
Умножив длину окружности на высоту получим площадь боковой стороны(S2) ведра(цилиндра):
S2=125,6*45=5652 см
Так как на 100 см^2 нужно 10г краски, значит на 10 см^2 нужен 1г краски. Масса необходимой краски:
m= 5652/10= 565,2 г