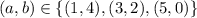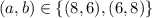DD1 = R /2.
Отсюда O1D = 2 R /3 − R /2 = R /6 . Так как АD = ½ AC = R √3 /2, то
ответ. R √7/3
1.2. B треугольнике AOB (рис. P.1.2) известны: ∠ BAO = α/2 , ∠ AOB = α/2 + π/2, BO = m· По теореме синусов находим AB = m ctg α/2· Теперь можно найти AC и R = ВО1:
AC = 2AD = 2АВ sin (π/2 − α) = 2АВ cos α = 2m ctg α/2 cos α,
ответ.
1.3. Условие задачи может быть геометрически осуществлено в двух случаях (рис. Р.1.3, а), т. е. когда треугольник либо правильный, либо равнобедренный тупоугольный (докажите). Решить эту задачу можно сразу для обоих случаев. На рис. Р.1.3, б изображены треугольник ABC и треугольник А1В1С1, составленные из средних линий первого треугольника. Треугольник А1В1С1 подобен треугольнику ABC с коэффициентом подобия половина. Следовательно, радиусы окружностей, описанных около этих треугольников, относятся как один к двум.
1.4. Если сторона а треугольника ABC биссектрисой АА1 разделена на отрезки а1 и а2, то можно записать следующие соотношения (рис Р. 1.4.):
Решая эту систему уравнений относительно a1 и а2, получим
Вычислим аналогично отрезки, на которые разделены стороны b и с треугольника ABC:
Так как отношение площадей треугольников, имеющих общий угол, равно отношению произведений сторон, между которыми лежит этот общий угол, то
Аналогично находим
Теперь найдем отношение
ответ.
1.5. Выразим площадь треугольника ABC через радиус r вписанной окружности и углы А, B и С треугольника.
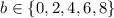.![a+b \in [0, 17]](/tpl/images/0491/3461/49ba3.png)
(т.к. максимальное значение a - это 9, а максимальное значение b - это 8, потому что b должно быть четным)![S \in [13, 30]](/tpl/images/0491/3461/88cd2.png)
![S = 9*m, S \in [13,30]](/tpl/images/0491/3461/fc309.png)
, то S = 18 или S=27
