ответ: S=1/3 кв. ед.
Пошаговое объяснение:
Решая уравнение (x+1)⁴=x+1, находим x1=-1 и x2=0 - нижний и верхний пределы интегрирования. Искомая площадь S=S1-S2, где S1=∫√(x+1)*dx, а S2=∫(x+1)²*dx. Находим первообразную для S1: F1(x)=∫(x+1)^(1/2)*d(x+1)=2/3*(x+1)^(3/2)+C1, где C1 - произвольная постоянная. Отсюда S1=F1(x2)-F1(x1)=2/3 кв. ед. Находим теперь первообразную для S2: F2(x)=∫(x+1)²*d(x+1)=1/3*(x+1)³+C2, где С2 - также произвольная постоянная. Отсюда S2=F2(x2)-F2(x1)=1/3 кв. ед. и тогда S=2/3-1/3=1/3.
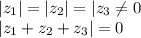
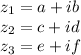
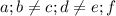
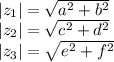
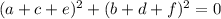
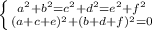
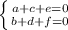
и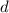 
с данного уравнения и подставим в выражение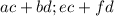 
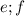и подставим в выражения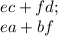 
, 
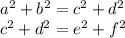
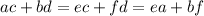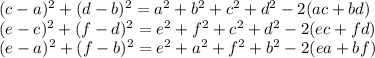
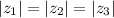
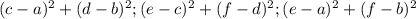- есть стороны длины и они как доказали равны , то есть удовлетворяют равенству сторон , а это в свою очередь равносторонний треугольник.
