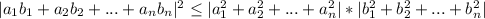
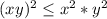 .
.
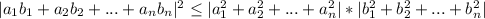 ).
). 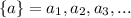 и
и 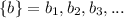 , так вот Буняковский доказывает что перемножив попарно элементы последовательностей и возведя результат в квадрат - получим результат меньший, чем если бы посчитали квадраты элементов обеих последовательностей по отдельности и перемножили. *
, так вот Буняковский доказывает что перемножив попарно элементы последовательностей и возведя результат в квадрат - получим результат меньший, чем если бы посчитали квадраты элементов обеих последовательностей по отдельности и перемножили. * (всё, что написано выше - верно и для него).
(всё, что написано выше - верно и для него).
v = S : t = 700 : 25 = 28 (км/ч) - скорость
ответ: 28 км/ч