Пошаговое объяснение:
Расстояние между пунктами 300 км.
Направление движения: на встречу друг другу.
Выехали из двух городов одновременно.
Скорость второго автомобиля на 6 км/ч меньше скорости первого автомобиля.
Время движения 1,5 ч.
Определить скорость автомобиля.
Расстояние, на которое сближаются автомобили за единицу времени, называют скоростью сближения vсб.
В случае движения автомобилей навстречу друг другу, скоростью сближения равно: vсб = v1 + v2
Если начальная расстояние между пунктами равна S километров и машины встретились через tвстр ч, то S = vсбл * tвстр = (v1 + v2) * tвстр, км.
Пусть скорость второго автомобиля равна х км/ч, тогда скорость первого автомобиля будет (х + 6) км/ч.
Согласно условию задачи, нам известно, что расстояние между пунктами S = 300 км и tвстр = 1,5 ч, подставим значения в формулу:
(х + (х + 6)) * 1,5 = 300
(2х + 6) * 1,5 = 300
3х + 9 = 300
3х = 300 – 9
3х = 291
х = 291 : 3
х = 97
Скорость второго автомобиля равно 97 км/ч.
Скорость первого автомобиля равно 97 + 6 = 103 км/ч.
ответ: скорость первого автомобиля — 103 км/ч; скорость второго автомобиля — 97 км/ч.
1)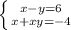
x-y=6
x=6+y 6+у+6у+у^2=-4
у^2+7у+10=0
у1= -2
у2= 5
х1= 6+2= 8
х2= 6-5 = 1
ответ: (8; -2) ; (1;5)
5)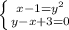
у-х+3=0
-х=-3-у
х= 3-у 3-у-1=y^2
-у^2-у+2=0
y^2+y-2=0
y1= 1
y2= -2
x1= 3-1 = 2
x2= 3+2 = 5
ответ: (2;1) ; (5;-2)
3)
x-y=1
-y=1-x
y= x-1 x^2-2x+2-26=0
x^2-2x-24=0
x1= 6
x2= -4
y1= 6-1 = 5
y2= -4-1 = -1
ответ: (6;5) ; (-4; -1)