Пошаговое объяснение:
Дано: F(x) = (x²-2*x+1)/(x + 1)
ИССЛЕДОВАНИЕ.
1. Область определения: D(y)= X≠ -1 , X∈(-∞;-1)∪(-1;+∞)
(x+1 ≠ 0. X ≠ -1
Не допускаем деления на 0 в знаменателе.
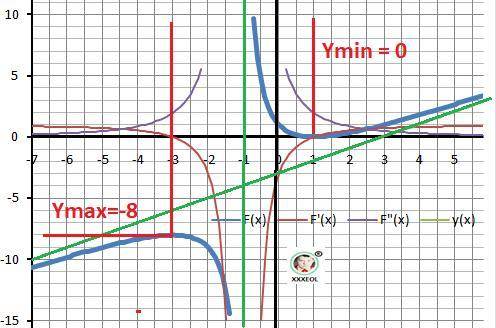
2. Разрыв II-го рода при Х = -1 Вертикальных асимптота - Х = -1
3. Пересечение с осями координат.
а) Нули функции, пересечение с осью ОХ.
Решаем квадратное уравнение в числителе. y=x²-2*x+1 = 0.
Дискриминант D = 0, Корни: x1 = x2 = 1
б) Пересечение с осью ОУ. У(0) = 1
4. Интервалы знакопостоянства.
Отрицательна: Y(x)≤0 - X∈(-∞;-1)∪[1]
Положительна: Y>0 - X∈(-1;1)U(1;+∞).
6. Проверка на чётность.
Есть сдвиг по оси ОХ - нет симметрии ни осевой ни центральной.
Функция общего вида - ни чётная, ни нечётная.
7. Поиск экстремумов по первой производной.
F'(x) =(2*x -2)/(x+1) - (1*(x²-2*x+1) = (x² +2*x -3)/(x+1)²
Решаем квадратное уравнение в числителе (x² +2*x -3) = 0
Дискриминант D = 16, Корни: x1 = -3, x2 = 1
8. Локальный максимум: y(-3) = -8, минимум: y(1) = 0.
9. Интервалы монотонности.
Возрастает: X∈(-∞;-3)∪(1;+∞).
Убывает: X∈(-3;-1)∪(-1;1).
10. Поиск перегибов по второй производной.
y''(x) = ?
Точки перегиба нет, кроме разрыва при х =-1
11. Выпуклая - (горка) - X∈(-∞;-1); Вогнутая - (ложка) X∈(-1;+∞;),
12. Наклонная асимптота: k = lim(+∞)Y(x)/x = 1 - наклон
b = lim(+∞)Y(x) - k*x -3/1 = -3 и y(x) = x -3 - асимптота.
12. Область значений. E(y) - y∈(-∞;+∞).
13. График функции на рисунке в приложении.
Пошаговое объяснение:
Дробь имеете числитель (число, что сверху) и знаменатель (число, что снизу). Для того чтоб сложить или отнять дроби нужно чтобы их знаменатель был одинаковым. В этих примерах знаменатель везде одинаковый. Значит нужно просто складывать или отнимать числитель, а знаменатель оставлять неизменным.
421.
1) 1/9 + 4/9 = (1+4)/9=5/9
2) 7/8 - 3/8 = (7-3)/8 = 4/8, эту дробь можно сократить для этого числитель и знаменатель нужно разделить на одинаковое число, в данном случае это 4
4/8=(4÷4)/(8÷4)=1/2
3) 15/19 - 6/19 = (15-6)/19=9/19
4) 5/16 + 1/16 = (5+1)/16 = 6/16, сокращаем на 2
6/16 = (6÷2)/(16÷2)=3/8
5) 3/14 + 11/14 = (3+11)/14=14/14, сокращаем на 14
14/14=(14÷14)/(14÷14)=1/1=1
6) 11/21+4/21=(11+4)/21=15/21, сокращем на 3
15/21=(15÷3)/(21÷3)=5/7
422.
1) 2/5+3/5=(2+3)/5=5/5=1
2) 3/7-2/7=(3-2)/7=1/7
3) 7/20 - 3/20=4/20 = (4÷4)/(20÷4)=1/5
4) 1/9+5/9=(1+5)/9=6/9=(6÷3)/(9÷3)=2/3
5) 6/23-2/23=(6-2)/23=4/23
6) 3/20+7/20=(3+7)/20=10/20=(10÷10)/(20÷10)=1/2
7) 13/29-2/29=(13-2)/29=11/29
8) 11/51 + 13/51=(11+13)/51=24/51=(24÷3)/(51÷3)=8/17
9) 17/72-13/72=(17-13)/72=4/72=(4÷4)/(72÷4)=1/18
10) 32/55+23/55=(32+23)/55=55/55=(55÷55)/(55÷55)=1/1=1
11) 5/33+6/33=(5+6)/33=11/33=(11÷11)/(33÷11)=1/3
12) 13/48 - 11/48=(13-11)/48=2/48=(2÷2)/(48÷2)=1/24