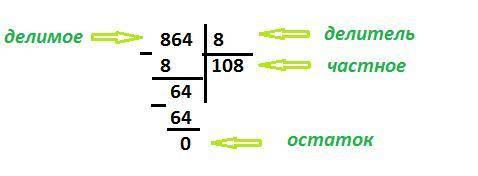
1) Первая цифра 8 делится на 8 нацело, записываем в частное 1.
1 · 8 = 8 → записываем под старшей 8 в числе 864 и вычитаем.
8 - 8 = 0
2) Сносим вниз следующую цифру 6 из числа 864. 6 < 8, на 8 поделить нельзя. Записываем в частное 0.
3) Сносим вниз следующую цифру 4 из числа 864. 64 делится на 8 нацело. Записываем в частное 8.
8 · 8 = 64 → записываем под числом 64 и вычитаем.
64 - 64 = 0
Все цифры числа 864 снесены вниз и поделены, деление закончено. Остаток равен нулю. Частное равно 108.
864 : 8 = 108
t∈(-∞;-9] ∪ [0;1/5]
Пошаговое объяснение:
t(t−1\5)(9+t)≤0 - решаем классическим методом интервалов. Неравенство представлено в каноническом виде (переменная минус число). Найдём корни, при которых каждый множитель обращается в ноль:
0; 1/5; -9
Расположим их в порядке возрастания на числовой оси - получим 4 интервала. Посчитаем в каждом из них знак неравенства - слева направо знаки:
"-","+","-" и "+", выбираем интервалы, на которых знак "минус" поскольку знак неравенства ≤0, получаем интервал:
t∈(-∞;-9] ∪ [0;1/5]
3-3х+5х+10=1-4х
2х+4х=1-3-10
6х=-12
х=-2
ответ:-2
3(2-х)-(5х+4)=0,4 - 16х
6-3х-5х-4=0,4-16х
-8х+16х=0,4-6+4
8х=-1,6
х=-0,2
ответ:-0,2