Пошаговое объяснение:
а) 4,8,12,16…;
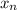 =4n
=4n
б) 1,-1,1,-1….
 =
=
2. Последовательность задана в аналитической форме yn=2n+10
Найти 10,50,63 член последовательности.
y₁₀=2·10+10=30
y₅₀=2·50+10=110
y₆₃=2·63+10=136
3. Последовательность задана в аналитической форме yn=n² +2.
Найти 5,10,13 член последовательности.
y₅=5²+2=25+2=27
y₁₀=10²+2=102
y₁₃=13²+2=171
4. Последовательность задана в рекурсивном виде y1=5
y n =y n-1 −3 , если n=2,3,4…
Найти 5,11,12 член последовательности.
y₅=y₄-3=y₃-3-3=y₂-3-3-3=y₁-3-3-3-3=y₁-4·3=5-4·3=-7
y₁₁=y₁₀-3=...=y₁-(11-1)·3=5-10·3=-25
y₁₂=y₁₁-3=...=y₁-(12-1)·3=5-11·3=-28
Это арифметическая прогрессия с разностью -3. Несложно доказать преобразуя данное рекурсивное соотношение
5. Последовательность задана в рекурсивном виде y 1 =3, y 2 =8 , y n =2y n-2 +3,
если n=3,4,5…. Найти 3,4,9 член последовательности.
y₃=2y₁+3=2·3+3=9
y₄=2y₂+3=2·8+3=19
y₅=2y₃+3=2·9+3=21
y₆=2y₄+3=2·19+3=41
y₇=2y₅+3=2·21+3=45
y₈=2y₆+3=2·41+3=85
y₉=2y₇+3=2·45+3=93
На последнем озере село половина всех гусей и еще полгуся и оказалось, что это все летевшие гуси. Значит, полгуся — это половина всех гусей, подлетевших к последнему озеру, а всего их было 0,5·2=1 гусь. На предпоследнем озере село половина всех гусей, подлетевших к нему, и еще полгуся, а еще один гусь полетел на последнее озеро. Значит, к этому озеру подлетело (1 + 0,5)·2=3 гуся. Рассуждая таким образом дальше, получим, что к пятому озеру подлетело 7 гусей, к четвертому — 15 гусей, к третьему — 31 гусь, ко второму — 63 гуся и, наконец, к первому — 127 гусей.
И всё )!
a^x((a-1)^x-2a)-((a-1)^x-2a)) <= 0
(a^x-1)((a-1)^x-2a) <= 0
Общность решения
1. {a^x<=1 {(a-1)^x>=2a
2. {a^x>=1 {(a-1)^x<=2a
Отсюда получаем 4 случая
1)
При a<0 , получаем что решений нет, так как основание логарифма (a) отрицательное (решения только в целых числах)
2)
При 0<a<1 получаем что основание логарифма (a-1) так же отрицательное
3)
При 1<=a<2 получаем
(-oo;log(a-1)(2a)) U (0;+oo)
4)
При a>=2
Получаем
x>=0 x<=log(a-1)2a
5)
Откуда [0,log(a-1)2a]
log(a-1) 2a = 2
2a=(a-1)^2
2a=a^2-2a+1
a>1
a^2-4a+1=0
D=12
a=(4+2√3)/2 = 2+√3
При a=2+√3 множество решений [0,2]