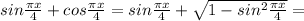Математика: Нужна производная от ln^2х знаю что ответ 2lnx/x

Нужна производная от ln^2х знаю что ответ 2lnx/x

👇

Увидеть ответ

Ответ:

olesiadukova

26.12.2022

2 сносится как степень, остаётся ln(x), затем производная от ln(x) -- 1/x
итого 1/x*ln(x)*2

4,6(45 оценок)

Открыть все ответы

Ответ:

solomijahladij6

26.12.2022

Вообще, уравнение проще решить графическим но для анализа функции её хорошо бы продифференцировать.
Поскольку задача указана для средней школы, то решим задачу в лоб, что длиннее.
Для начала нужно выкинуть cos из уравнения, чтобы можно было заменой уйти от тригонометрических функций.
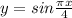$sin \frac{ \pi x}{4} + cos \frac{ \pi x}{4} = sin \frac{ \pi x}{4} +\sqrt{1-sin^{2}\frac{ \pi x}{4} } =$ /Замена $y=sin \frac{ \pi x}{4}$ /
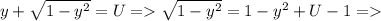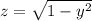= $y+ \sqrt{1-y^{2} } =U=\sqrt{1-y^{2} } =1-y^{2} + U -1=$ /Замена $z=\sqrt{1-y^{2} }$ /
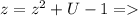
=> $z=z^{2} +U-1=
$
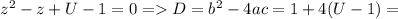
=> $z^{2}-z +U-1=0 = D=b^{2} -4ac=1+4(U-1)=$
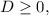В случае, если $D \geq 0,$ то уравнение имеет решение.
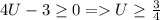=> При $4U-3 \geq 0 = U \geq \frac{3}{4}$ ;
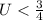То есть при $U <\frac{3}{4}$ , решений нет.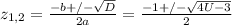
$z_{1,2} = \frac{-b +/- \sqrt{D} }{2a} =\frac{-1 +/- \sqrt{4U-3} }{2}$
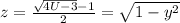
Поскольку z - это корень, то по определению корня это неотрицательное число => $z = \frac{\sqrt{4U-3} -1}{2}=\sqrt{1-y^{2}}$

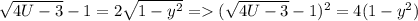
=> $\sqrt{4U-3} -1=2\sqrt{1-y^{2}}=(\sqrt{4U-3} -1)^2=4(1-y^{2})$
=> $4U-3-2\sqrt{4U-3} +1=4-4y^{2} = 4y^{2} = 6-4U +2 \sqrt{4U-3}$
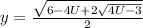
=> $y = \frac{\sqrt{6-4U +2 \sqrt{4U-3}}}{2}$
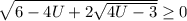При этом должно выполняться неравенство $\sqrt{6-4U +2 \sqrt{4U-3}} \geq 0$ , иначе корней нет. Пометим это выражение (1*)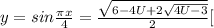

$y=sin \frac{ \pi x}{4}=\frac{\sqrt{6-4U +2 \sqrt{4U-3}}}{2}[$
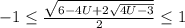
Решения есть, если $-1\leq \frac{\sqrt{6-4U +2 \sqrt{4U-3}}}{2} \leq 1$

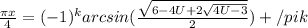=> $\frac{ \pi x}{4}=(-1)^k arcsin(\frac{\sqrt{6-4U +2 \sqrt{4U-3}}}{2})+/pi k$ , где k принадлежит Z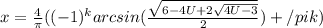
=> $x=\frac{4}{ \pi }( (-1)^k arcsin(\frac{\sqrt{6-4U +2 \sqrt{4U-3}}}{2})+/pi k)$
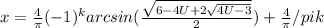
=> $x=\frac{4}{ \pi }(-1)^k arcsin(\frac{\sqrt{6-4U +2 \sqrt{4U-3}}}{2})+\frac{4}{ \pi } /pi k$
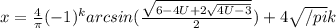
=> $x=\frac{4}{ \pi }(-1)^k arcsin(\frac{\sqrt{6-4U +2 \sqrt{4U-3}}}{2})+4 \sqrt{/pi} k$
Поскольку мы ищем наименьший корень, то что числитель должен быть наименьшим при минимальном k либо максимальным при минимальном k, найденные числа необходимо сравнить => Найдём сначала наименьшее значение
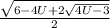Выражение $\frac{\sqrt{6-4U +2 \sqrt{4U-3}}}{2}$ должно быть наименьшим
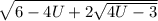=> Выражение $\sqrt{6-4U +2 \sqrt{4U-3}}$ должно быть наименьшим
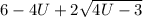=> Выражение $6-4U +2 \sqrt{4U-3}$ должно быть наименьшим
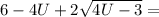$6-4U +2 \sqrt{4U-3}=$ /Замена k=4U-3/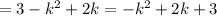 =3-k^2 +2 k= -k^2+2k+3

Это формула параболы с ветвями, направленными вниз с вершиной при k=1. При этом вспомним, что в выражении (1*) мы требуем, чтобы данное выражение было $\geq 0$
=> Наименьших значений это выражение будет достигать в точках пересечения с 0
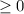
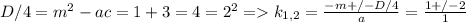
=> $D/4=m^2-ac= 1+3=4=2^2 =k_{1,2} = \frac{-m+/-D/4}{a}= \frac{1+/-2}{1}$
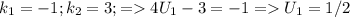
$k_{1} =-1; k_{2} =3; = 4U_{1}-3=-1 = U_{1}=1/2$
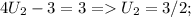
=> $4U_{2}-3=3 = U_{2} = 3/2;$
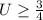Поскольку у нас ограничения для $U\geq\frac{3}{4}$ , то минимальное значение будет достигаться при U=3/2;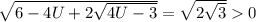
Проверим это значение U ещё вот по этому ограничению :
$\sqrt{6-4U +2 \sqrt{4U-3}}=\sqrt{2\sqrt{3}} 0$
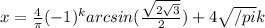
=> $x=\frac{4}{ \pi }(-1)^k arcsin(\frac{\sqrt{2\sqrt{3}}}{2})+4 \sqrt{/pi} k$
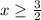$x \geq \frac{3}{2}$ - это следует из условий задачи
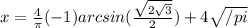=> k=1 => $x=\frac{4}{ \pi }(-1) arcsin(\frac{\sqrt{2\sqrt{3}}}{2})+4 \sqrt{/pi}$ (11)
Вообще, нужно ещё доказать, что минимальное значение арксинуса в сумме с слагаемым при k=1 меньше, чем максимальное значение арксинуса при k=0.
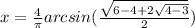
Арксинус максимален в вершине параболы описывающей его числетель => U=1 => $x=\frac{4}{ \pi } arcsin(\frac{\sqrt{6-4 +2 \sqrt{4-3}}}{2})$
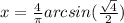
=> $x=\frac{4}{ \pi } arcsin(\frac{\sqrt{4}}{2})$
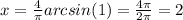
=> $x=\frac{4}{ \pi } arcsin(1) = \frac{4 \pi}{ 2\pi }=2$

Теперь определим, которое из чисел меньше. Вычтем из x (11) 2:
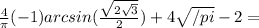
$\frac{4}{ \pi }(-1) arcsin(\frac{\sqrt{2\sqrt{3}}}{2})+4 \sqrt{/pi} -2=$
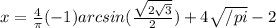
= $x=\frac{4}{ \pi }(-1) arcsin(\frac{\sqrt{2\sqrt{3}}}{2})+4 \sqrt{/pi} -2$
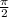/Для упрощения оценки допустим, что арксинус достигает своего максимального значения = $\frac{ \pi }{2}$ , /
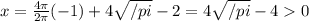
= $x=\frac{4 \pi}{ 2\pi }(-1) +4 \sqrt{/pi} -2=4 \sqrt{/pi}-40$
Следовательно x=2 - это минимальный корень из всех возможных.
ответ: x=2

Просто кошмар, это решение стоит намного больше, чем
Прилагаю график, на котором изображена функция tex]sin \frac{ \pi x}{4} + cos \frac{ \pi x}{4}[/tex], а также y=x, которая служит ограничением по условиям задачи

4,6(44 оценок)

Ответ:

Masha36127

26.12.2022

1)У пшеницы вырастают длинные ости, такие жесткие волоски. Это мешает животным их есть.
По происхождению они придаточные, как и опорные корни, начинающиеся у некоторых злаков еще над землей. Закреплению растения в почве часто кущение, образование множества прикорневых побегов, составляющих рыхлую или плотную, кочковидную дерновину. Обычно на корни приходится основная масса злака, иногда до 90%. Такая корневая система, эффективно поглощающая и накапливающая воду выживать в условиях регулярного стравливания травоядными животными, периодических засух и степных пожаров. Цветки. Цветки мелкие, малозаметные, без четко выраженного околоцветника. Лепестки и чашелистики, вероятно, представлены одной или несколькими миниатюрными чешуйками, которые называются цветковыми пленками, или лодикулами, и расположены под тычинками. Цветок обычно обоеполый, т.е. содержит и тычинки, и пестик. Пестик состоит из завязи с двумя (реже - тремя) столбиками, несущими длинные перистые рыльца. Тычинок обычно три - с длинными, свешивающимися из цветка нитями и продолговатыми пыльниками.

4,4(63 оценок)

Это интересно:

Компьютеры-и-электроника

18.09.2022

Как добавить кнопку Facebook на свой сайт: шаг за шагом...

Транспорт

14.01.2023

Как избежать аварий на дороге...

Компьютеры-и-электроника

17.04.2020

Создание онлайн веб каста с помощью Windows Media Encoder...

Транспорт