1клетка=1см
S-площадь
1)Рисунок где изображена трапеция:
S=1/2(a+b)*h
a-верхнее основание
b-нижнее основание
h-высота
a=8
b=18
h=6
S=1/2(8+18)*6=78см^2
2)Рисунок с фигурой, похожий на букву П:
S=1+1+12+2+18+18=52см^2 (для того чтобы найти площадь я разбил фигуру на несколько треугольников и прямоугольников, а потом сложил все их площади)
3)Рисунок с Фигурой, похожий на букву Ц:
S=2+12+12+6=32см^2(алгоритм решения такой же как и в задании 2)
4)на рисунке изображена прямоугольная трапеция:
S=1/2(a+b)*h
a=3
b=6
h=6
S=1/2(3+6)*6=4,5*6=27см^2
Правильный ответ:
1)78см^2.
2)52см^2.
3)32см^2
4)27см^2.
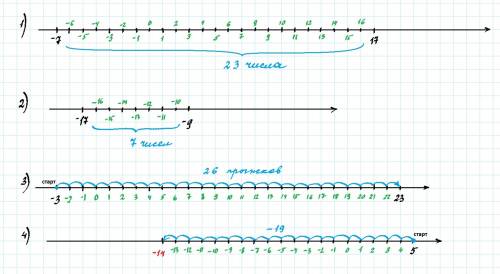
1) На координатном луче отмечаем точки (-7) и (17). Затем отмечаем все точки, лежащие между данными и соответствующие целым числам (смотри рис. 1). Считаем их количество. Получается 23.
Второй И еще из результата (24) вычитаем 1, т.к. одну крайнюю точку - (17) - учитывать не нужно..
24-1 = 23
ответ: 23
2) Чертим координатную прямую и отмечаем на ней точки (-17) и (-9). Затем отмечаем все точки между данными, соответствующие целым числам (см. рис. 2). Считаем их количество. Получается 9 чисел.
Либо можно сосчитать так: -9-(-17) = -9+17 = 8 – это количество чисел от (-17) до (-9), не считая (-17).
Убираем еще одно число, т.к. (-9) тоже не нужно учитывать.
8-1 = 7
ответ: 7
3) Кузнечик стартует в точке (-3), а в точке 23 останавливается.
Все целые числа он должен проходит по порядку. Ему необходимо прыгать только вправо. Тогда количество прыжков будет наименьшим. Если он сделает хоть один прыжок назад, это увеличит общее количество прыжков (см. рис. 3).
В этом случае от (-3) до 23 кузнечик сделает 23-(-3)=23+3=26 прыжков.
ответ: 26
4) Чертим числовую прямую. Отмечаем на ней точки, соответствующие целым числам. От точки (5) отсчитываем 19 целых чисел влево, т.к. нужно вычесть 19.
Оказываемся в точке (-14) (см. рис. 4)
ответ: -14
у=2745