78 (единиц)
Пошаговое объяснение:
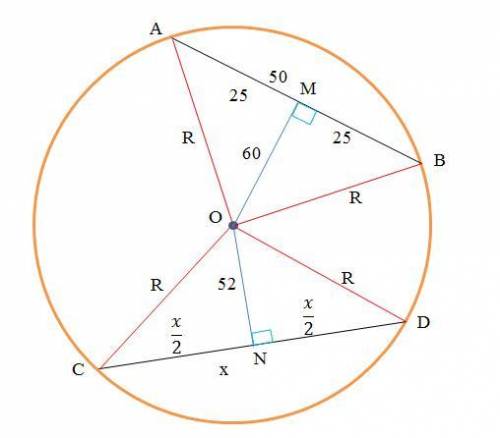
Дано (см. рисунок):
Окружность радиуса R
AB=50 – длина первой хорды
OM=60 – расстояние от центра O окружности до хорды AB
ON=52 – расстояние от центра O окружности до хорды CD
Найти: x=CD – длину второй хорды
Решение.
Так как OA=OB=OC=OD и равны радиусу R окружности, то получаем равнобедренные треугольники OAB и OCD. По условию, расстояние от центра O окружности до хорды AB, то есть длина отрезка OM, перпендикулярного к отрезке AB, равно 60. Точно также, расстояние от центра O окружности до хорды CD, то есть длина отрезка ON, перпендикулярного к отрезке CD, равно 52.
Но, по свойству равнобедренных треугольников, перпендикуляры OM и ON к основанию равнобедренных треугольников, соответственно, OAB и OCD является высотой, медианой и биссектрисой. Тогда медианы OM и ON делят, соответственно, основание равнобедренных треугольников OAB и OCD пополам. Отсюда получаем:
1) длина MB=50:2=25 и длина ND=x:2;
2) треугольники OMB и OND прямоугольные с гипотенузой, равной радиусу R.
Применим теорему Пифагора к прямоугольному треугольнику OMB и находим R:
R² = OM²+MB² = 60²+25² = 3600+625 = 4225 = 65² или R=65.
Применим теорему Пифагора к прямоугольному треугольнику OCD:
R² = ON²+ND² = 52²+(x:2)² или
(x:2)² = R²–52² = 65²–52² = 4225–2704 = 1521 = 39² или
x:2 = 39.
Отсюда CD=x=39·2 = 78 (единиц).
12,5y=1
y=1:12,5
y=0,08
Проверка
32,1*0,08-19,6*0,08=1
1)32,1*0,08=2,568
2)19,6*0,08=1,568
3)2,568-1,568=1
В)2,3y+2,5y=36
4,8y=36
y=36:4,8
y=7,5
Проверка
2,3*7,5+2,5*7,5=36
1)2,3*7,5=17,25
2)2,5*7,5=18,75
3)17,25+18,75=36
С) 4,2*(0,25+х)=1,47
0,25+х=1,47:4,2
0,25+х=0,35
х=0,35-0,25
х=0,1
Проверка
4,2*(0,25+0,1)=1,47
1)0,25+0,1=0,35
2)4,2*0,35=1,47