Пошаговое объяснение:
Частное положительного и отрицательного чисел отрицательно, так ли это: *
да+
При делении любых двух отрицательных чисел частное имеет знак:
“плюс”
Частное двух отрицательных чисел равно частному их модулей, так ли это: *
да
Укажите верные утверждения: а) частное положительного и отрицательного чисел отрицательно; б) произведение трех отрицательных чисел отрицательно; в) при умножении отличного от нуля числа на -1 получается противоположное число;
г) частное двух отрицательных чисел равно частному их модулей. *
а, б, в, г
Вычислите: –6,4 : 0,4 *
–16
Вычислите: (-12,8) : 4 *
-3,2
Вычислите: 5,7: (–0,3) *
-19
-253: (-11) *
23
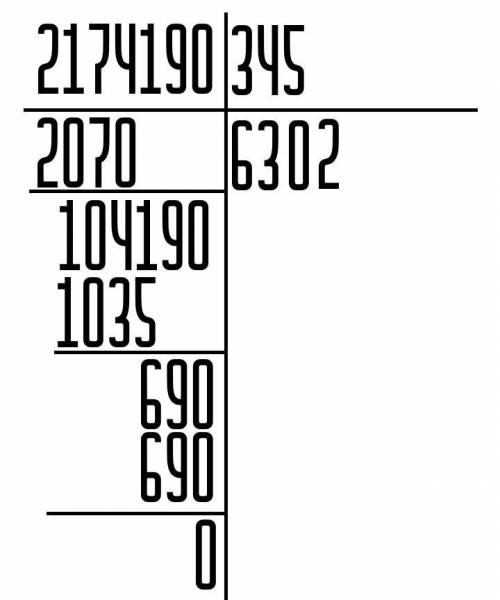
(Файл со столбиком я прикрепил)
1) Для начала мы подбираем кол-во цифр от начала, для определения первого множителя:
2174 - это число
2) Подбираем максимально приближённое значение (оно обязательно меньше данного) множителя на 345, для достижения 2174:
6 - такое число
6 · 345 = 2070
2174 - 2070 = 104 - запишем данное число ниже
3) Спускаем следующие число и получаем 1041. По аналогии со вторым действием подбираем число:
3 - такое число
3 · 345 = 1035
1041 - 1035 = 69 - запишем данное число ниже
4) Можно заметить, что нам не хватает цифр, потому пишем ноль и получаем число 690, а далее выполним те же махинации:
2 - такое число
2 · 345 = 690
690 - 690 = 0 - пример решен
ответ: 6302.
1) АМ - вектор, равный половине вектора АК, АК=АВ+АС .
Складываем векторы по правилу параллелограмма.
Точка М - середина диагоналей параллелограмма АВКС, точка их пересечения. Смотри рис. 1.
2) 1/2*АС - это вектор АК ; АВ-1/2*АС=АВ-АК=КВ
Теперь выполним параллельный перенос вектора КВ, точку К совместим с точкой А, тогда точка В перейдёт в точку М. Смотри рис. 2.
3) Пользуемся правилом треугольника сложения векторов: АВ+ВС=АС.
Теперь к АС нужно прибавить такой вектор, чтобы получить нулевой вектор. Его длина должна быть равна 0, а начало нулевого вектора совпадает с его концом. Но АС-СА=0, то есть в качестве вектора СМ надо взять вектор СА. Точка М совпадает с точкой А .
АВ+ВС+СМ=0. Смотри рис. 3.
4) 4*СМ=3*АС+2*ВС ⇒ СМ=3/4*АС+2/4*ВС=3/4*АС+1/2*ВС
ВК=1/2*ВС , АР=3/4*АС
Выполним параллельный перенос вектора ВК , совместив точку В с точкой А, получим вектор АР=ВК.
Сложим по правилу параллелограмма АК+АР=AD .
Выполним параллельный перенос вектора AD так, чтобы точка А совпала с точкой С. Тогда точка D перейдёт в точку М. Получим вектор СМ=АР. Смотри рис. 4.