Задана функция 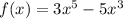
1) Найдем область определения функции:
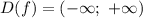 , то есть
, то есть 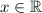
2) Исследуем функцию на четность:
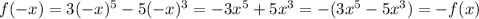
Функция нечетная, непериодическая.
3) Найдем точки пересечения графика функции с осями координат:
Если 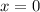 , то
, то 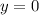 , значит
, значит 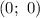 — точка пересечения с осью
— точка пересечения с осью 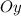 .
.
Если 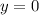 , то есть
, то есть 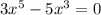 , то:
, то:

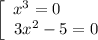
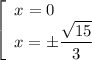
Значит 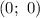 ,
, 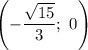 и
и 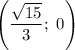 — точки пересечения с осью
— точки пересечения с осью 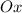 .
.
4) Асимптот данная функция не имеет, поскольку она непрерывная на всей области определения.
5) Найдем производную и критические (стационарные) точки функции:

Из уравнения 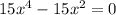 имеем критические точки:
имеем критические точки:
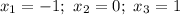
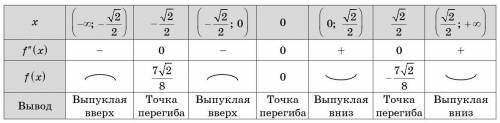
6) Найдем промежутки возрастания, убывания и экстремумы функции, заполнив таблицу (см. вложение).
7) Исследуем функцию на выпуклость и точки перегиба с второй производной:
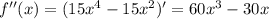
Если на промежутке 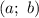 дифференцируемая функция
дифференцируемая функция 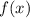 имеет положительную вторую производную, то есть
имеет положительную вторую производную, то есть 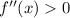 для всех
для всех 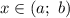 , то график этой функции на
, то график этой функции на 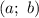 является выпуклым вниз; если на промежутке
является выпуклым вниз; если на промежутке 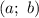 дифференцируемая функция
дифференцируемая функция 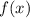 имеет отрицательную вторую производную, то есть
имеет отрицательную вторую производную, то есть 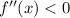 для всех
для всех 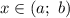 , то график этой функции на
, то график этой функции на 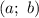 является выпуклым вверх.
является выпуклым вверх.
Решим уравнение: 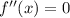
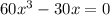
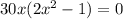
Имеем корни: 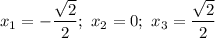
Систематизируем данные, полученные по второй производной, в таблице (см. вложение)
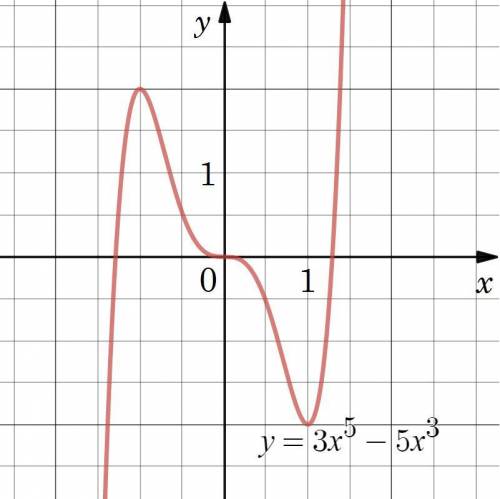
8) Изобразим график заданной функции (см. вложение).
9) Из графика можем найти область значений функции:
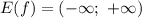 , то есть
, то есть 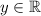

ответ:
) в знаменателе находится многочлен.
2) многочлены находятся и в числителе и в знаменателе.
3) один или оба многочлена могут быть под корнем.
4) многочленов и корней, разумеется, может быть и больше.
пошаговое объяснение:
основные же предпосылки для применения признака даламбера следующие:
1) в общий член ряда («начинку» ряда) входит какое-нибудь число в степени, например, , , и так далее. причем, совершенно не важно, где эта штуковина располагается, в числителе или в знаменателе – важно, что она там присутствует.
2) в общий член ряда входит факториал. с факториалами мы скрестили шпаги ещё на уроке числовая последовательность и её предел. впрочем, не помешает снова раскинуть скатерть-самобранку: