пусть первый кусок сплава х кг, тогда процент золота в нем
3/x*100=300/x %
второй сплав тогда 40-х кг и процент золота в нем
15/(40-x)*100=1500/(40-x)
тогда если содержание золота в первом сплаве на 40% меньше чем во втором. запишу это уравнением
1500/(40-x)-300/x=40
привожу все о общему знаменателю x(40-x), тогда в числителях будет
1500 x-300(40-x)=40(40-x)x
1500x-12000+300x=1600x-40x^2
40x^2+200x-12000=0
делю все на 40
x^2x+5x-300=0
D=25+1200=1225=35^2
x=(-5+35)/2=15
отрицательный х не подходит
ответ первый сплав 15 кг
f(x)=1/3 x^3-x^4+5
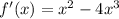
найдём стационарные точки:
х²-4х³ = 0
х²*(4х-1) = 0
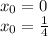
Достаточное условие наличия экстремума в точке - производная меняет знак при переходе. Найдём значения производной на интервалах (возьмём значения: 1(0<0.25<1) , 1/5(0<1/5<1/4) и -1 (-1<0<1/4)
f'(1) = 1² - 4*(1³) = -3
f'( 1/5) = 0,2² - 4*(0,2³) = 0,04 - 4*(0,008) = 0,008 (Знак поменялся, точка 0,25 - точка минимума)
f'(-1) = (-1)²-4*(-1)³ = 1-4*(-1) = 1 + 4 = 5 знак остался прежним, поэтому точка экстремума Одна
ответ: х = 0,25 - точка экстремума
Вот самый простой пример: цилиндр.
Берем прямоугольник и начинаем вращать его вокруг одной из сторон.
Смотри
Было Вращаем Стало
А теперь гораздо хитрее. Бывает так, что ось вращения находится далеко от фигуры, которая вращается.
Например, так
Вращаем
Что получится? Бублик. А по научному ТОР.
Ну и так вот можно любую фигуру вертеть вокруг любой оси, и будут получаться разные более или менее сложные тела вращения.
Ну, а поверхность вращения – это просто граница тела вращения. Ведь поверхность это всегда граница тела.Здесь мы рассмотрим подробно несколько тел вращения. Те, которые встречаются в школьных задачах. Это шар, цилиндр и конус.
ШарШар – тело вращения, полученное вращением полуокружности вокруг диаметра.Было Вращаем Стало
Вообще-то есть и другое определение шара – через ГМТ (геометрическое место точек)
Шар – геометрическое место точек, удаленных от одной фиксированной точки на расстояние, не более заданного.Скажу тебе по секрету, что хоть второе определение и пугающее на вид, оно удобнее в обращении. Задумайся, ведь если тебя попросят сказать, что такое шар, ты скажешь что-то вроде
«ну …там есть центр и радиус…, подразумевая, что все точки внутри шара находятся я на расстоянии не большем, чем радиус.
Ну, в общем, шар он и есть шар.
Названия, которые ты должен знать:
Незнакомое тебе, наверное, только одно.
Диаметральное сечение шара – сечение, проходящее через центр. Это сечение иногда еще называют большим кругом.А вообще:
Любое сечение шара – круг.Граница шара называется сфера. (Так же, как граница круга – окружность.)Площадь поверхности сферыSповерхности=4πR2Sповерхности=4πR2RRR - радиусОткуда взялось? Умные математики придумали – это не так уж просто – придется просто запомнить.
Объем шараVшара=43πR3Vшара=43πR3RRR - радиусЭто еще одна хитрая формула, которую придется запомнить, не понимая, откуда она взялась.
Если ты знаком с производной, то можешь заметить это
Vшара=SповерхностиVшара=SповерхностиИ это не случайно! Но почему это так вышло, мы тоже здесь обсуждать не будем – читай теорию для сильного уровня.
ЦилиндрЦилиндр – тело, образованное вращением прямоугольника вокруг одной из сторон.Вообще – то полное имя этого тела «прямой круговой цилиндр», но составители задач и мы вместе с ними по дружбе называем его просто цилиндром. Названия, относящиеся к цилиндру, такие:
Основания у цилиндра – это круги
Еще у цилиндра есть так называемая развертка.
Представь, что у нас от цилиндра осталась только боковая поверхность, и мы ее разрезали вдоль образующей и развернули.Что получится? Представь себе, прямоугольник.
Развертка цилиндра – прямоугольник.
Площадь поверхности цилиндраПлощадь боковой поверхностиSбок.=2πRHSбок.=2πRHRRR - радиусHHH - высота, она же образующая.Откуда взялась эта формула? Это как раз легко! Именно потому, что цилиндр можно развернуть, и получится прямоугольник 2πR⋅H2\pi R\cdot H2πR⋅H.
Площадь этого прямоугольника и есть площадь боковой поверхности цилиндра. Площадь прямоугольника, как мы хорошо помним равна произведению сторон, поэтому Sбок.=2πRHSбок.=2πRHПлощадь полной поверхности цилиндраПрибавляем теперь площадь двух кругов – оснований и получаем
Sполн.=2πRH+2πR2Sполн.=2πRH+2πR2Можно вынести (хотя и не обязательно) 2πR2\pi R2πR:
Sполн.=2πR(H+R)Sполн.=2πR(H+R)
Но эту формулу неудобно запоминать!
Гораздо проще запомнить, что полная поверхность – сумма боковой поверхности и еще двух кругов – оснований, а боковая поверхность – прямоугольник. И тогда Sполн.Sполн. можно вообще не запоминать, ты всегда сам напишешь, что
Sполн.=2πRHпрямоугольник+2πR2два кругаSполн.=2πRH⏟прямоугольник+2πR2⏟два круга
Объем цилиндраV=πR2HV=\pi {{R}^{2}}HV=πR2HRRR - радиус основанияHHH - высотаЭто точно как у призмы и параллелепипеда
V=Sоснования⋅HV=Sоснования⋅H, только у призмы и параллелепипеда SоснованияSоснования - это площадь многоугольника, а у цилиндра SоснованияSоснования - это площадь круга.
КонусКонус – тело вращения, образованное вращением прямоугольного треугольника вокруг одного из катетов.Было Вращаем Стало
И опять же, полное название этого тела: «прямой круговой конус», но во всех задачах у нас говорится просто «конус».