
Пусть 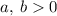 Тогда
Тогда 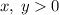 . Также, т.к. корень - число неотрицательное, то
. Также, т.к. корень - число неотрицательное, то 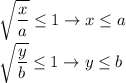 .
.
Теперь заменим  на противоположное число
на противоположное число 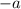 . Заметим, что теперь
. Заметим, что теперь 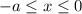 и каждому значению функции, соответствующее каждому значению аргумента, соответствует противоположный аргумент. Проведя аналогичные действия для
и каждому значению функции, соответствующее каждому значению аргумента, соответствует противоположный аргумент. Проведя аналогичные действия для 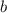 , заметим, что изменение знака параметров на противоположные лишь отображает график относительно координатных осей, но не меняют длину кривой. Тогда достаточно найти длину кривой для положительных
, заметим, что изменение знака параметров на противоположные лишь отображает график относительно координатных осей, но не меняют длину кривой. Тогда достаточно найти длину кривой для положительных 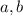 , а затем в получившейся формуле заменить
, а затем в получившейся формуле заменить  на
на 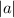 ,
, 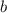 на
на 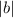 .
.
Теперь запишем параметрическое задание функции.
Пусть 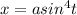 . Тогда
. Тогда 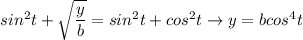 ,
, ![t\in[0;\dfrac{\pi}{2}]](/tpl/images/0672/7264/77f83.png) .
.
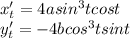
Вычисление длины кривой на фото 1 и 2. На 3 фото вычисление вс интеграла.
Теперь остается лишь подставить модули параметров. Получаем 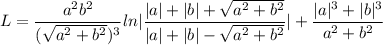
![Вычислить длину дуги кривой при интеграла [tex] \sqrt{ \frac{x}{a} } + \sqrt{ \frac{y}{b} } = 1[/tex](/tpl/images/0672/7264/e9be8.jpg)
![Вычислить длину дуги кривой при интеграла [tex] \sqrt{ \frac{x}{a} } + \sqrt{ \frac{y}{b} } = 1[/tex](/tpl/images/0672/7264/56c30.jpg)
![Вычислить длину дуги кривой при интеграла [tex] \sqrt{ \frac{x}{a} } + \sqrt{ \frac{y}{b} } = 1[/tex](/tpl/images/0672/7264/2da60.jpg)