ответы к/р 4 "делимость чисел"
Вариант 1
1. а) Д(33)=1;3;11;33.
б) Д(13)= 1;13.
2. К(14)= 14;28;42;56;70;…
3. а) 4302, 2880, 9164, 6020
б) 7385, 2880, 6020
в) 2880, 6020
4. а) 5532, 6786
б) 6786
5.а) да
б) да
6. а)105=3∙5∙7
б) 360=2332∙5
7. а)НОД(32;48)=16
б) НОК(16;20)=80
8. 11(ост.15)
9. а) 2194
б) 945
10.9996
Вариант 2
1. а) Д(27)=1;3;9;27.
б) Д(19)= 1;19.
2. К(15)= 15;30;45;60;75;…
3. а) 9164, 1810, 3976, 870
б) 1810, 1235, 870
в) 1810, 870
4. а) 5649, 1827
б) 1827
5.а) да
б) нет
6. а)105=2∙3∙17
б) 360=2233∙5
7. а)НОД(27;45)=9
б) НОК(15;18)=90
8. 17(ост.35)
9. а) 1040
б) 141
10. 1005
ДАНО: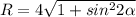 
- функция, r = 4 - окружность,
НАЙТИ: Площадь фигуры вне окружности.²
Пошаговое объяснение - решение силой Разума.
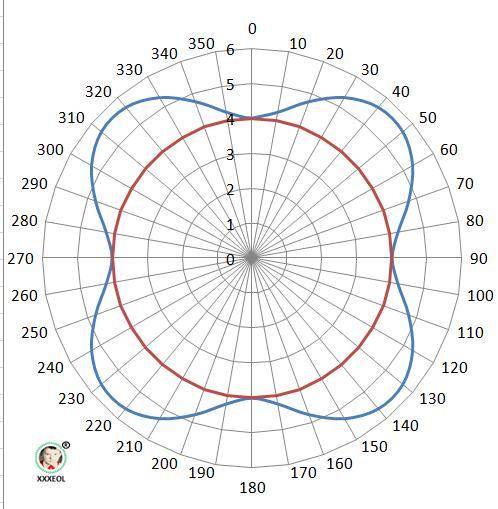
Мысль 1. Задача в полярных координатах. Построение графика без использования дополнительных средств весьма затратно.
Рисунок с графиком функции при расчёте через 10° в приложении.
Мысль 2. Площадь фигуры - разность площадей функции и окружности с r= 4.
Мысль 3. Площадь окружности по формуле: S1 = π*r² = 16π - (запоминаем - потом надо вычесть).
Мысль 4. Площадь ограниченная функцией по формуле:
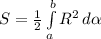
Пределы интегрирования от а = 0, до b = 2π - запоминаем.
Мысль 5. Вычисляем значение R(α)²
R(α)² = 16*(1 + sin²2α).
Коэффициент 16 выносим из под интеграла и приступаем собственно к интегрированию.
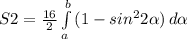
Делаем подстановку - sin²x = (1-cos2x)/2 и получаем новый интеграл.
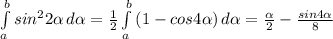
В результате получили функцию площади .
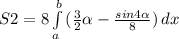
Вычисляем на границах интегрирования.
S2(2π) = 8*3π = 24π и S2(0) = 0 и
S2 - 24*π - площадь функции.
И переходим к ответу - вычитаем площадь центрального круга.
S = S2 - S1 = 24*π - 16*π = 8π (ед.²) - площадь фигуры - ответ.
Вопрос неполный, поэтому ответов может быть несколько.
Если можно использовать не все цифры, то
1) наименьшее натуральное число 1
Если все цифры должны быть использованы единожды, то
2) наименьшее натуральное 137
3) наименьшее целое число -731
4) наименьшее рациональное положительное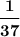
5) наименьшее рациональное десятичное положительное 1,37
и т.д. Можно придумать ещё много разных наименьших чисел.
Как правило, в подобных задачах речь идёт о натуральных числах, все цифры используются и не повторяются. Тогда
ответ : 137