Исключаем четвертого поставщика и меняем на 50% от первого завода.
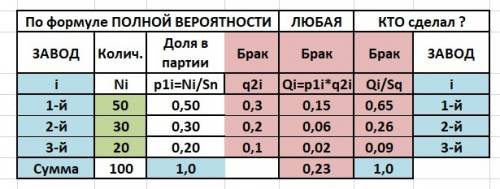
Решение сведено в таблицу. Таблица в приложении.
Задача состоит из двух событий - И случайно выбрать любой блок И этот блок - бракованный.
Вероятность выбора любого блока = Р1 - дана - (0,5 и 0,3 и 0,2).
Вероятность брака от любого завода = Р2 - дана - (0,3 и 0,2 и 0,1)
Вероятность события А - сумма произведений вероятностей каждого. Брак - это плохо - обозначаем Q.
Qi = 0.15(1зав) +0.06(2зав) +0.02(3зав) = 0.23 всего брак - ОТВЕТ а)
Вероятность кто изготовил этот брак находим по формуле Байеса.
Брак первого завода - 0,15 из 0,23 или 0,65 - ОТВЕТ б)
Надо пройтись 3 раза, делов-то!
![\left[\begin{array}{cccccccc}1&2&3&4&5&6\\3&5&2&4&6&1\end{array}\right] \left[\begin{array}{cccccccc}1&2&3&4&5&6\\3&5&2&4&6&1\end{array}\right] \left[\begin{array}{cccccccc}1&2&3&4&5&6\\3&5&2&4&6&1\end{array}\right]](/tpl/images/0921/8845/141de.png)
Например, для 1. 1 переходит в 3, потом 3 переходит в 2, потом 2 переходит в 5. Так что 1 переходит в 5. И так далееИмеем