1) Чтобы не запутаться, обозначим расходы бензина на автобазах буквами, соответствующими названиями автобаз:
А - расход бензина на автобазе А
Б - расход бензина на автобазе Б
В - расход бензина на автобазе в
2) Анализируем условие задачи.
Так как на автобазе А расход бензина на 10% больше, чем на автобазе Б, то можем записать первое уравнение:
А = 1,1*Б
Так как на автобазе В расход бензина на 40% меньше, чем на автобазе А, то есть он составляет 60% от расхода автобазы А, то можем записать второе уравнение:
В = 0,6*А
3) Подставляем второе уравнение в первое получаем:
В = 0,6*А = 0,6*1,1*Б = 0,66*Б
Таким образом расход бензина на автобазе В составляет 66% от расхода бензина на автобазе Б, то есть меньше на 34%.
ответ: меньше на 34%
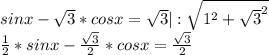
Допустим, 1/2 и √3/2 это sin и cos какого-то угла. Это возможно если выполняется основное тригонометрическое тождество, то есть когда этот угол определён на тригон. круге. Проверяем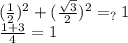 
Да всё верное, обозначим этот угол как α=arcsin(1/2)+2pi*n, n∈Z. Стоит отметить, что т.к. и синус и косинус этого угла положительны, то этот угол может лежать исключительно в 1 четверти.
Тогда у нас есть -sinα*sinx+cosα*cosx= -√3/2
Левую часть можно представить как косинус суммы.
cos(α+x)= -√3/2.
cos(arcsin(1/2)+2pi*n+x)= -√3/2, n∈Z. 2Pi*n можно сократить так как это целые круги и значение косинуса ни как не поменяется. И тогда сразу берём arccos.
arcsin(1/2)+x= ±5pi/6+2pi*k, k∈Z. Раскрываем arcsin т.к. это табличное значение и мы его знаем, ну я точно.
x= ±5pi/6-pi/6+2pi*k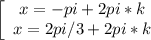, k∈Z.
k∈Z.
ответ: x={-pi+2pi*k; 2pi/3+2pi*k}. k∈Z.
40-10=30% - меньше на автобазе В по сравнению с Б