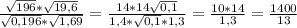y=e⁻²ˣ+e²ˣ-2·x³-3·x
Пошаговое объяснение:
Дано линейное уравнение и начальные условия:
y''-4·y=8·x³, y(0)=2, y'(0)=-3
1) Сначала решаем линейное однородное уравнение
y''-4·y=0
Для этого составим и решим характеристическое уравнение:
λ²-4=0 ⇔ (λ+2)(λ-2)=0 ⇔ λ₁ = -2, λ₂ = 2
Получены два различных действительных корня, поэтому общее решение однородного уравнения:
y=C₁·e⁻²ˣ+C₂·e²ˣ
2) Теперь найдём частное решение y₁ неоднородного уравнения
y''-4·y=8·x³
Так как правая часть уравнения многочлен 8·x³, то будем искать в виде
y₁=A·x³+B·x²+C·x+D
Найдём первую и вторую производную:
y₁'=(A·x³+B·x²+C·x+D)=3·A·x²+2·B·x+C
y₁''=(3·A·x²+2·B·x+C)'=6·A·x+2·B
Подставим y₁ и y₁'' в левую часть неоднородного уравнения:
6·A·x+2·B-4·(A·x³+B·x²+C·x+D)=8·x³
Раскрываем скобки и упростим:
-4·A·x³-4·B·x²+(6·A-4·C)·x+2·B-4·D=8·x³
Приравниваем коэффициенты при соответствующих степенях и составим систему линейных уравнений и решаем:
-4·A=8 ⇒ A = -2
-4·B=0 ⇒ B = 0
6·A-4·C=0 ⇒ 4·C = 6·A ⇒ 4·C = 6·(-2) ⇒ 4·C = -12 ⇒ C = -3
2·B-4·D=0 ⇒ 4·D=2·B ⇒ 4·D=2·0 ⇒ D = 0
Получили частное решение
y₁= -2·x³-3·x
3) Тогда получим следующее общее решение
y=C₁·e⁻²ˣ+C₂·e²ˣ-2·x³-3·x
4) Применим начальные условия:
y(0)=C₁·e⁰+C₂·e⁰-2·0³-3·0=2 ⇒ C₁+C₂=2
y'=(C₁·e⁻²ˣ+C₂·e²ˣ-2·x³-3·x)'= -2·C₁·e⁻²ˣ+2·C₁·e²ˣ - 6·x²-3
y'(0)= -2·C₁·e⁰+2·C₂·e⁰ - 6·0²-3 = -3 ⇒ -2·C₁+2·C₂ - 3=-3 ⇒ C₁ -C₂ =0 ⇒ C₁=C₂
Получили систему линейных уравнений и решаем:
C₁ = C₂ =1
C₁ + C₂ =2 ⇒ C₂ + C₂ =2 ⇒ 2· C₂ =2 ⇒ C₂ =1
5) Подставляя C₁ и C₂ в общее решение получим
y=e⁻²ˣ+e²ˣ-2·x³-3·x
1)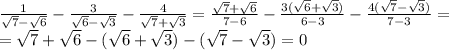
2) 2a^2 - 5ab + 2b^2 = a^2 - 4ab + 4b^2 + a^2 - ab - 2b^2 = (a-2b)^2 + (a-2b)(a+b) = (a-2b)(a-2b+a+b) = (a-2b)(2a-b)
При a = √7+√6; b = √7-√6 получается:
2a^2 - 5ab + 2b^2 = (a-2b)(2a-b) = (√7+√6-2√7+2√6)(2√7+2√6-√7+√6) = (3√6-√7)(3√6+√7) = 9*6 - 7 = 54 - 7 = 47
3)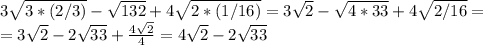
4)