1) Установим с линейки расстояние между ножками циркуля 4 см 5 мм = 4,5 см;
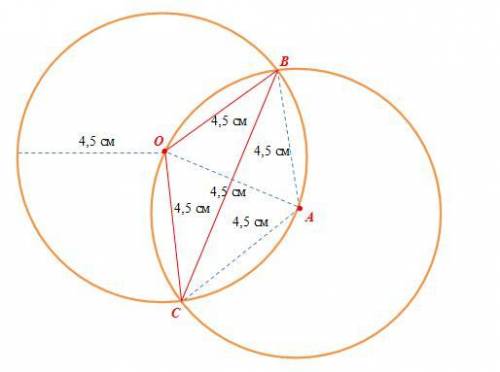
2) Отметим на бумаге произвольную точку и обозначим через О (см. рисунок);
3) Проводим окружность с центром в точке О радиуса 4,5 см;
4) Выберем любую точку окружности, например, точку А и проводим окружность с центром в точке А радиуса 4,5 см;
5) Точки при пересечении окружностей обозначим В и С;
6) Точку О соединим с точками В и С с линейки отрезками;
7) Соединим отрезком с линейки точки В и С.
Построенный треугольник ОВС является решением задачи.
Докажем это:
а) Длины отрезков ОВ и ОС равны 4,5 см как длина радиуса окружности;
б) Так как длины отрезков ОВ, ОС, ОА, ВА, СА равны длине радиуса, то треугольники ОВА и ОСА равносторонние. У равносторонних треугольников все углы равны 60°. Тогда ∠ВОА=60° и ∠СОА=60°, откуда ∠СОВ=∠ВОА+∠СОА=120°.
Что и требовалось.
50дм=500см
50дес>400ед
260с<3ч
20сут<2400ч