2. Угол при основании равнобедренного треугольника АВС равен 32º, АВ -его боковая сторона, АМ- биссектриса треугольника. Найдите углы треугольника АВМ. (Рассмотрите два случая.)
1) ∠В=180º - 32º*2 = 116º
Так как АМ – биссектриса ∠ВАМ=32:2=16º
∠АМВ=180 – 116-16=48º
2) Из Δ АМС ∠ АМС= 180 – 32-16= 132º
∠АМВ и ∠АМС смежные, значит ∠АМВ=180-132=48º
∠В= 180º- ∠ВАМ -∠АМВ =180-48-16=116º
3. К прямой т проведены перпендикуляры АВ и СD. Докажите, что ∆ АВD=∆ CDB, если AD = BC.
АВ и СD перпендикуляры, значит ∠ ВDС и ∠ АВD =90 º . В четырехугольнике АВDС два угла прямоугольные, а диагонали равны AD = BC. Значит АВDС – прямоугольник. У прямоугольника противоположные стороны равны.
АВ=СD , AD = BC, ВD – общая сторона.
∆ АВD=∆ CDB по трем равным сторонам.
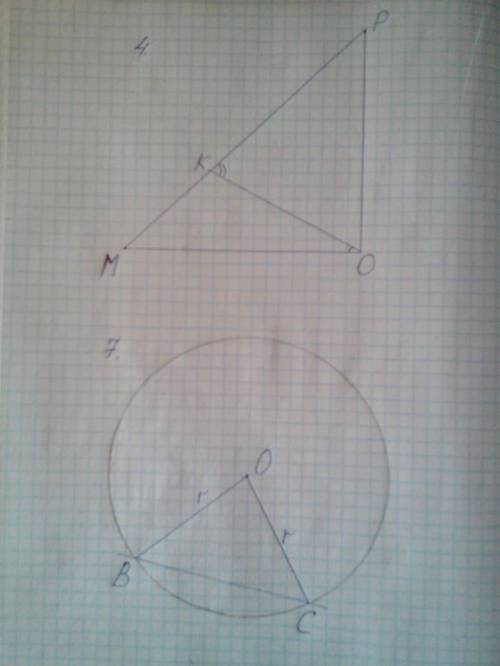
4. В равнобедренном прямоугольном треугольнике MOP на гипотенузе МP отмечена точка К. Известно, что ∠OKP в 4 раза больше, чем ∠МОК. Найдите углы треугольника МОК.
Δ МОК прямоугольный равнобедренный.
∠М=∠Р = 90º:2=45º
∠ОКР=4*∠МОК
Из теоремы о внешних углах ∠М= ∠ОКР-∠МОК
∠М= 4*∠МОК-∠МОК=3∠МОК
∠МОК = 45º:3=15º
∠ МКО=180º - 45º -15º = 120º
Или ∠МКО= 180º - 4*15º=120º
7. В окружности с центром О проведена хорда ВС. Найдите ∠OВС и ∠ВOС, если один из них на 36 º больше другого.
Δ ОВС равнобедренный ВО=ОС= r , значит прилежащие к основанию углы равны.
∠OВС=∠OСВ =хº
2х+х+36 =180
3х = 144
х = 48
∠OВС=∠OСВ =48º
∠ВOС= 48º+36º=84º

Пошаговое объяснение:
1. ( ) Найдите все делители числа 15
А) 15;
Б) 1, 3, 5, 15; правильный ответ
В) 1, 15;
Г) 3, 5, 15
2. ( ) Какое из предложенных чисел делится на 9
А) 112590 правилбный ответ
Б) 54215
В) 67802
Г)1212121
3. ( ) На какое число разделится значение суммы 45+55+105 без остатка
А) на 3;
Б) на 5; правильный ответ
В) на 9
Г) на 2
4. ( ) Какое из предложенных чисел делиться и на 2, и на 3
А) 123681
Б) 810331
В) 1620315 нет правильного ответа
Г) 2035112
5. ( ) Число 2343 делится на 3___ так как ___12 делится на __3__
6. ( ) Число 85236 делиться на _2__ так как оканчивается __на парные числа
7. ( ) Если один из ___двух делится на некоторое __число, то и второеделится на это число
8. ( ) Если одно слагаемое делится на 2, то и __сумма делится на это число
9. ( ) Если число оканчивается одной из цифр 0,2,4,6,8, то оно делится на 2, числа оканчивающиеся какой-нибудь из цифр _1,3,5,7,9, не делится на 2
10. ( ) Установите соответствие между числом и его свойством.
Число Свойство числа
1. 225 А. кратно 3 и 5
2. 8211 Б. кратно 5, не делится на 3
3. 1235 В. кратно 3
4. 1035 Г. ни кратно 2, ни 3
1 2 3 4
А В Б Г
11. ( ) Установите соответствие между числами и его делителями:
Число Делители числа
1. 125 А. 1, 3, 5, 9, 15, 27…
2. 510 Б. 1, 2, 3, 5, 15, 85…
3. 135 В. 1, 5, 25…
4. 612 Г. 1, 2, 3, 6, 12, 17, 36…
1 2 3 4
В Б А Г
12. ( ) Установите соответствие между числами и его разложением на простые множители:
Число Разложение на простые множители
1. 185 А. 2 в кубе умножить на три умножить на 13
2. 312 Б. 3 умножить 7 умножить 7
3. 366 В. 5 умножить 37
4. 147 Г. 2 умножить 3 на умножить 61
1 2 3 4
В А Г Б
Сначала найдем длину листа для боковой поверхности , она будет равна длине окружности основания
2πR = πD = 3.14 * 200 cм= 628 см = 6, 28 метра
4 * 6.28 =25.12 м² уйдет на боковую поверхность
Теперь найдем площадь обоих оснований.
Основание цистерны представляет собой круг диаметром 200 см.
200 см = 2м
Площадь круга вычисляется по формуле - πR².
Теперь найдем радиус . Он равен 2 \ 2 = 1 метр - радиус основания. Подставим значения в формулу
πR² = 3.14 * 1м² = 3.14 м² - площадь одного основания
3.14 * 2 = 6.28 м² площадь обоих оснований
25.12 + 6.28 = 31.4 м² жести уйдет на цистерну