это справедливо для неправильных дробей, т.е. когда числитель больше знаменателя.
Пошаговое объяснение:
а) Записываем исходное уравнение
7x-9=5x-17,
б) переносим неизвестные в левую часть, известные - в правую.
7x-5x=9-17,
в) Приводим подобные слагаемые
2x=-8,
г) Находим неизвестное с коэффициентом равным 1
x=(-8):2.
д) Фиксируем его.
x=-4.
е) Записываем ответ.
ответ: -4.
***
0,2y+2,3=0,7y-3,2;
Можно неизвестные вправо, а известные влево. Но это нестандартный подход к решению. Все равно неизвестные придется переносить влево.
2,3+3,2=0,7y-0,2y;
Приводим подобные слагаемые
5,5=0,5y;
Находим значение неизвестного
y=5,5:0,5;
Фиксируем его.
y=11;
Записываем ответ
ответ: 11.
1)если x больше 0:
x^2-5x больше 0
x(x-5) больше 0
т.к. х больше 0, то х-5 тоже больше 0, значит х больше 5. (это одна часть ответа - промежуток от 5 до + бесконечности. (не включая 5)
2) если x меньше 0
то модуль х равен (-х)
получаем:
x^2+5x больше 0
х(х+5) больше 0
т.к х меньше 0, то и х+5 меньше 0, значит х меньше (-5)
это второй промежуток решения : от - бесконечности до -5 (не включая -5)
3) 0 - легко подставить и понять, что решением не является
ответ: объединение двух промежутков: от - бескон. до -5 и от 5 до +бескон.
Да, достаточно рассмотреть случай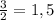
, переходящий в 
.
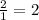Отсюда следует вывод, что действительно, дробь могла увеличиться