Швидкість велосипедиста на рівній поверхні становить 28 км/год. Швидкість велосипедиста в гору становить 14 км/год
Пошаговое объяснение:
Нехай швидкість велосипедиста на рівній місцевості х, тоді швидкість велосипедиста в гору місцевості х-14.
х>0;
х-14>0.
28/(х-14)+56/х=4
28х/х^2-14х+(56х-784)/х^2-14х=4
(84х-784)/(х^2-14х)=4
(84х-784)/(х^2-14х)-4=0
(84х-784)/(х^2-14х)-(4х^2-56х)/(х^2-14х)=0
84х-784-(4х^2-56х)=0. х^2-14х≠0
-4х^2+140х-784=0|/-4 x(x-14)≠0
х^2-35+196=0. x≠0 або х-14≠0
D=1225-784=441. х≠14
x1=(35+21)/2=28
x2=(35-21)/2=7
Швидкість велосипедиста по рівній поверхні 28 км/год або 7 км/год.
х-14>0
Нехай х=7 км/год, тоді
7-14>0
-7>0 х≠7
Нехай х=28 км/год, тоді
28-14>0
14>0
Відповідь:
Швидкість велосипедиста по рівній поверхні становить 28 км/год
Швидкість велосипедиста в гору становить 14 км/год
Перевірка :
28/14+56/28=4
2+2=4
4=4
Пошаговое объяснение:
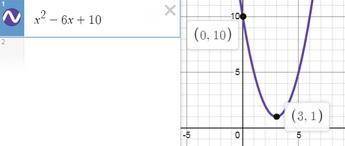
y=x²−6x+a это парабола ветвями вверх
у нас есть минимальное значение функции у = 1
мы пойдем путем, обратным пути поиска экстремума функции.
найдем, в какой точке достигается минимум (а минимум достигается в точке х0, где производная функции равна 0)
y'(x) = 2x -6 2x-6 = 0 ⇒ x = 3
таким образом вершина нашей параболы (ее минимум) достигается в точке (3; 1), т.е. парабола проходит через эту точку. отсюда найдем а
у(3) = 3²−6*3+a = 1 ⇒ а = 10
таким образом мы восстановили уравнение
у = x²−6x+10
тогда точка пересечения с осью ординат (0; 10) , а ее ордината
у = 10
85 минут -100% (85 минут все время)
x минут - 20% (х минут-время катания на велосипеде)
85*20/100=17 минут
ответ : 17 мин.