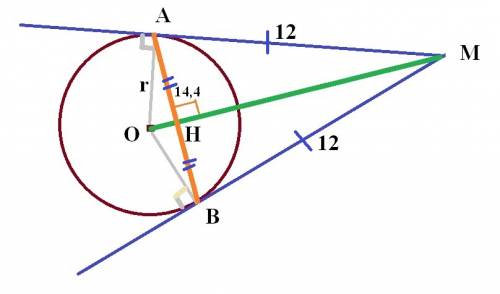
Чертеж во вложении.
Пусть МА и МВ - две касательные. О-центр окружности, ОА - радиус.
По свойству касательных ОА⊥МА, ОВ⊥МВ.
В силу равенства прямоугольных треугольников МОА и МОВ по гипотенузе и катету, углы АМО и ВМО также будут равны. Значит, MO- биссектриса угла АМВ и угла АОВ.
Пусть Н - точка пересечения биссектрисы МО и хорды АВ. Т.к. МА=МВ, то треугольник АМВ - равнобедренный, тогда МН-высота и медиана. Значит, АН=ВН=7,2 см.
В треугольнике АНМ по теореме Пифагора
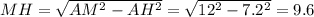
Т.к. АН-высота прямоугольного ∆ОАМ, то АН²=OH·НМ
7,2²=ОН·9,6
ОН=51,84/9,6=5,4
В треугольнике АНО по теореме Пифагора
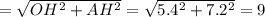
ответ: 9.
С2
т.к. прямые АВ1 и D1C скрещивающиеся, то угол между ними будет равен углу между прямыми A1B и AB1.
Диагонали ромба пересекаются под прямым углом. т.е. если O - точка пересечения диагоналей, то треуг. ABO - Прямоугольный и BO=1\2 BD=6, AO=1\2AC=3 По т. Пифагора можно найти сторону AB=√(36+9)=√45=3√5
По опр. tg можно найти tgAB1B=3√5\√15=3\√3=√3 По таблице tg находим, что угол AB1B=60гр. Т.к. A1B1BA - прямоугольник, то угол AB1B=B1BA=60 Если O1 - точка пересечения прямых A1B и B1A, то угол B1O1B - искомый и равен: 180-60-60=60
х=100*17/68=25