1. Нет, не получится. Представим, будто мы обкладываем поле доминошками. Каждая доминошка покрывает одно черное и одно белое поле, а при выкидывании полей a1 и h8 черных полей оказывается на 2 меньше, чем белых.
2. Решение Пусть искомое число abcd. Для каждой цифры a,b,c,d посчитаем, сколько раз она встречается в данных четырех числах. Очевидно, что сумма этих вхождений должна равняться 8. Поскольку никакая цифра не встречается в 3 числах, то каждая цифра встречается ровно дважды. Т.е. в искомом числе могут быть только цифры 0,1,3,4,6,7. Но в первом числе из этих цифр есть только 6 и 0. Значит, эти цифры в числе точно есть. Аналогично из третьего числа, получаем цифры 4 и 3. Составим табличку, в которой плюсики стоят в тех разрядах, в которых они могут быть написаны.
0 + − + −
3 − + − +
4 + − + −
6 + − − +
Т.к. в разряде сотен есть только один « + », то в разряде сотен числа стоит тройка. Действуя так далее и воспользовавшись тем, что четырехзначное число с нуля не начинается, получим число 4306, которое, очевидно, подходит. ответ 4306.
3. решение в файле
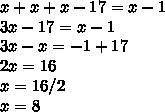
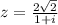
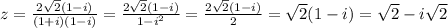
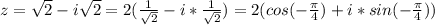
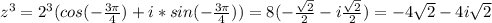
Оценка:
Так как каждый знаком не более, чем с восемью другими, каждая сплетница должна быть знакома хотя бы с одним сплетником, значит, сплетников не меньше 7. Пусть у нас 7 сплетников, тогда каждая из сплетниц знакома с одним сплетником (иначе кто-то новость не узнает), но так как каждый сплетник знаком не более, чем с восемью сплетницами, граф знакомств бьётся на 7 компонентов, значит, новость узнают не все. Значит, сплетников было не меньше восьми.
Пример:
Первый сплетник знает с 1-ой по 8-ую сплетниц, второй - с 8-ой по 15-ую, третий - с 15-ой по 22-ую, ... , восьмой - с 50-ой по 55-ую. Тогда для каждого сплетника найдётся сплетница, знающая хотя бы одного другого сплетника.
ответ: 55 сплетниц.