Это слова вида abcba.
Здесь вместо a, b, c могут быть любые латинские буквы, в том числе и одинаковые.
Всего в латинском алфавите 26 букв, поэтому будет
26*26*26 = 26^3 = 17576 вариантов.
Но должно быть хотя бы две разных буквы, поэтому 26 вариантов отпадает.
ответ: 17550.
48•36=1728 см²- площадь листа картона.
16•12=192 см² - площадь одной карточки.
48:16=3 (раза)
24:12=3 (раза)
1) Длина карточки три раза умещается по длине листа картона, а ширина карточки три раза умещается по его ширине
Поэтому данный лист можно разрезать на
3•3=9 карточек нужного размера, при этом не останется обрезков.
2) Из листа картона площадью 72•24=1728 см² девять карточек не получится, хотя его площадь больше площади одной карточки в 1728:192=9 (раз)
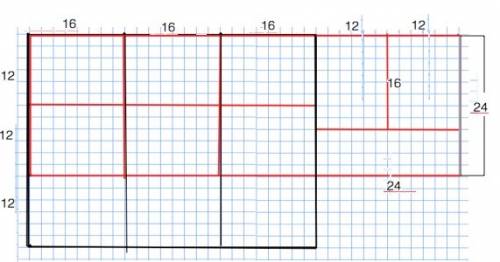
Как ни располагай линии разрезов, получится не больше 8 карточек, и останется кусок размером 24•8=192 см², т.е. площадью, равной площади одной карточки. (см. рисунок)
На рисунке черными линиями отмечен лист 48•36 см² и красными - лист размером 72•24 см²
Т.к. это палиндром, то будем рассматривать только первые 3 символа - вторая половина числа такая же, как и первая.
Тогда на первую позицию в рассматриваемом трехзначном числе будет 26 вариантов букв, на вторую анал. 26, и на третью так же 26. Тогда всего палиндромов из 5 букв : 26*26*26=17576. Но нам нужно, чтобы хотя бы 2 буквы были обинаковые, поэтому из общего кол-ва вычтем число палиндоромов с одинаковыми полностью буквами (т.е. на всех позициях только одна из букв лат.алф.), а их 26, тогда получаем: 17576-26=17550.
ОТВЕТ:17550.