4работник 1 категории и 6 работников 2 категории за смену изготовили 132,а 2 работника 1 категории и 5 работников 2 категории за смену изготовили 90 деталей.сколько деталей изготовил один работник каждой категории? 20

👇

Увидеть ответ

Ответ:

viktoiabekkknuv

26.05.2022

х - 1 категория

у - 2 категория

4х+6*у=132

2х+5у=90 *(-2)

4х - 4х + 6у -10у=132 - 180

4у=48

у= 12 деталей 2 категория

4х+6*12=132

4х=60

х= 15 деталей 1 категория

4,7(45 оценок)

Открыть все ответы

Ответ:

Слендер12

26.05.2022

ответ:-∞ < x < -6, 1 < x < +∞ функция возрастает -6 < x < 1

Пошаговое объясненПроизводная функции у = (х³/3)+(5x²/2)-6x+4 равна:

у = x² + 5x - 6.

Находим критические точки, приравняв производную нулю:

x² + 5x - 6 = 0.

Квадратное уравнение, решаем относительно x:

Ищем дискриминант:D=5^2-4*1*(-6)=25-4*(-6)=25-(-4*6)=25-(-24)=25+24=49;

Дискриминант больше 0, уравнение имеет 2 корня:x₁=(√49-5)/(2*1)=(7-5)/2=2/2=1;x₂=(-√49-5)/(2*1)=(-7-5)/2=-12/2=-6.

Исследуем значение производной вблизи критических точек:

х -6.5 -5.5 0.5 1.5

у 3.75 -3.25 -3.25 3.75.

Если производная меняет знак с + на -, то это максимум функции, если с - на +, то минимум.

На промежутках, где производная положительна, там функция возрастает, а где отрицательна - там функция убывающая

4,5(62 оценок)

Ответ:

olesyaprk

26.05.2022

№1.

а) 126 = 2 * 3 * 3 * 7

б) 84 = 2 * 2 * 3 * 7

№2.

Чтобы найти НОД нужно перемножить общие множители:

а) НОД (126; 84) = 2 * 3 * 7 = 42

Чтобы найти НОК, нужно к множителям бОльшего числа добавить недостающие множители и перемножить:

б) НОК (126; 84) = 2 * 3 * 3 * 7 * 2 = 252

№3.

Т.к. НОК (84; 126) = 42:

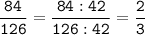
$\tt\displaystyle\frac{84}{126}=\frac{84:42}{126:42}=\frac{2}{3}$

№4.

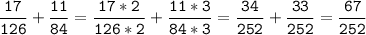
$\tt\displaystyle\frac{17}{126}+\frac{11}{84}=\frac{17*2}{126*2}+\frac{11*3}{84*3}=\frac{34}{252}+\frac{33}{252}=\frac{67}{252}$

№5.

$(\tt\displaystyle\frac{7}{15}+\frac{3}{10})*2\frac{14}{23}+1\frac{6}{57}:(\frac{7}{19}-\frac{30}{57})=(\frac{14}{30}+\frac{9}{30})*\frac{60}{23}+\frac{63}{57}:(\frac{21}{57}-\frac{30}{57})=\frac{23}{60}*\frac{60}{23}+\frac{63}{57}*(-\frac{57}{9})=2+(-7)=-5$

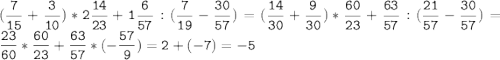
№6.

а) 105 = 3 * 5 * 7

б) 924 = 2 * 2 * 3 * 7 * 11

№7.

а) НОД (105; 924) = 3 * 7 = 21

б) НОК (105; 924) = 2 * 2 * 3 * 7 * 11 * 5 = 4620

№8.

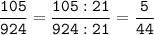
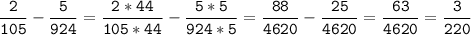
$\tt\displaystyle\frac{105}{924}=\frac{105:21}{924:21}=\frac{5}{44}$

№9.

$\tt\displaystyle\frac{2}{105}-\frac{5}{924}=\frac{2*44}{105*44}-\frac{5*5}{924*5}=\frac{88}{4620}-\frac{25}{4620}=\frac{63}{4620}=\frac{3}{220}$

№10.

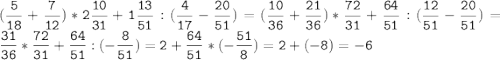
$(\tt\displaystyle\frac{5}{18}+\frac{7}{12})*2\frac{10}{31}+1\frac{13}{51}:(\frac{4}{17}-\frac{20}{51})=(\frac{10}{36}+\frac{21}{36})*\frac{72}{31}+\frac{64}{51}:(\frac{12}{51}-\frac{20}{51})=\frac{31}{36}*\frac{72}{31}+\frac{64}{51}:(-\frac{8}{51})=2+\frac{64}{51}*(-\frac{51}{8})=2+(-8)=-6$

№11.

а) 630 = 2 * 3 * 3 * 5 * 7

б) 252 = 2 * 2 * 3 * 3 * 7

№12.

а) НОД (630; 252) = 2 * 3 * 3 * 7 = 126

б) НОК (630; 252) = 2 * 3 * 3 * 5 * 7 * 2 = 1260

№13.

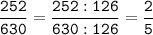
$\tt\displaystyle\frac{252}{630}=\frac{252:126}{630:126}=\frac{2}{5}$

№14.

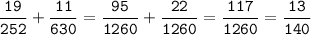
$\tt\displaystyle\frac{19}{252}+\frac{11}{630}=\frac{95}{1260}+\frac{22}{1260}=\frac{117}{1260}=\frac{13}{140}$

№15.

$(\tt\displaystyle\frac{5}{14}+\frac{10}{21})*3\frac{3}{5}+1\frac{1}{6}:(\frac{13}{22}-\frac{25}{33})=(\frac{15}{42}+\frac{20}{42})*\frac{18}{5}+\frac{7}{6}:(\frac{39}{66}-\frac{50}{66})=\frac{35}{42}*\frac{18}{5}+\frac{7}{6}*(-\frac{66}{11})=3+(-7)=-4$