все в картинках........-----
Понятие производной сложной функции
Пусть y – сложная функция x, т.е. y = f(u), u = g(x), или
Если g(x) и f(u) – дифференцируемые функции своих аргументов соответственно в точках x и u = g(x), то сложная функция также дифференцируема в точке x и находится по формуле
Типичная ошибка при решении задач на производные - машинальное перенесение правил дифференцирования простых функций на сложные функции. Будем учиться избегать этой ошибки.
Посмотрите на формулу 9 в таблице производных. Исходная функция является функцией от функции, причём аргумент x является аргументом лишь второй функции, а вторая функция является аргументом первой функции, или, согласно более строгому определению - промежуточным аргументом по независимой переменной x.
А теперь посмотрите на картинку ниже, которая иллюстрирует решение задач на сложные производные по аналогии с простым примером из кулинарии - приготовлении запечёных яблок, фаршированных ягодами.

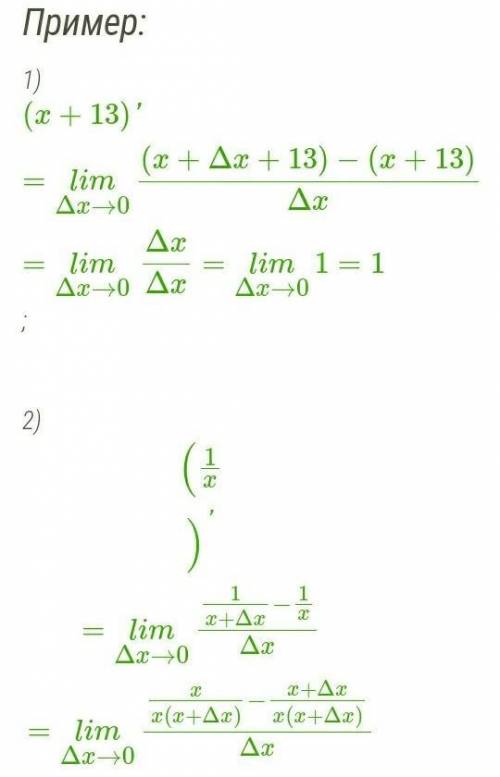

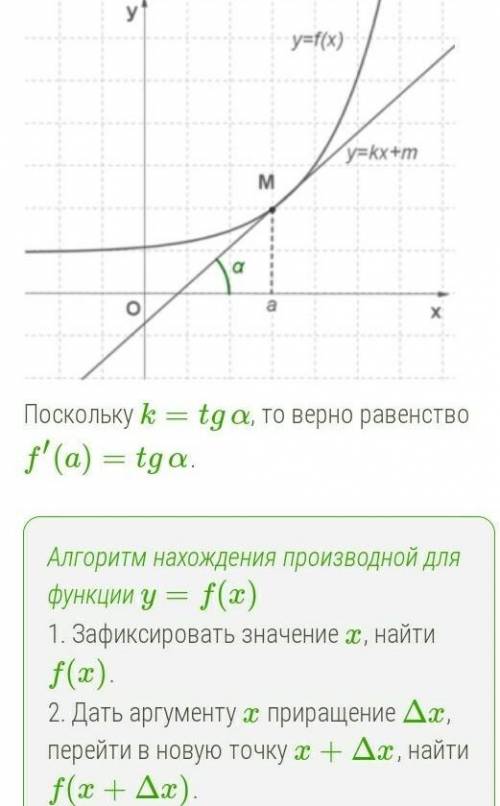

Пошаговое объяснение:
Чтобы найти 1-е слагаемое, надо из суммы вычесть 2-слагаемое
х+3,2=17,1
х=17,1 - 3,2
х= 13,9
13,9+3,2=17,1
17,1=17,1
Неизвестно вычитаемое. Из уменьшаемого вычитаем разность.
46,9-у=2,19
у= 46,9-2,19
у= 44,71
46,9-44,71=2,19
2,19=2,19
Усложненное уравнение: Левую сторону, скобку оставляем , а из разности вычитаем вычитаемое. И получаем простое уравнение. Дальше решаем аналогично первому уравнению.
(2,46+а)-4,2=6,43
2,46+а= 6,43+4,2
2,46+а= 10,63
а= 10,63 -2,46
а= 8,17
(2,46+8,17)-4,2=6,43
6,43=6,43
. начертить координатную прямую.
чтобы не делать это каждый раз, нам разрешили-посоветовали на обороте обыкновенной деревянной линейки посередине провести прямую.
примерно по середине отметить точку начала 0. и приняв за единицу 1см. отложить влево и вправо от нуля несколько делений.
теперь смотрим от (-1) до нуля одно деление ; от 0 до 2 еще 2 деления- всего три.
аналогично между (-4) и 3 7 ; между (-5) и 1 6
скоро будете учить
ПРАВИЛО:
из координаты правой точки (-2) вычесть координату левой точки (-3)
-2+3=3-2=1