Пошаговое объяснение:
Задача 1.
1. После понижения цены на 10%, билет станет стоить:
35*0,9=31,5 руб
2. На 120 рублей можно будет купить:
120:31,5=3,8 ⇒ 3 билета.
ответ: 3 билета.
Задача 2.
1. (4-3i)/(2+i)=(4-3i)(2-i)/(2+i)(2-i)=(8-4i-6i-3i²)/(4-i²). Т.к. i²=-1, делаем замену:
(8-10i-3*(-1))/(4-(-1))=(8-10i+3)/5=(5-10i)/5=5(1-2i)/5=1-2i
2. (1+i)³=1³+3*1²*i+3*1*i²+i³=1+3i+3i²+i³. Т.к. i²=-1, делаем замену:
1+3i+3*(-1)+(-1)*i=1+3i-3-i=-2+2i
3. i³-i¹⁰⁰=i²*i-(i²)⁵⁰. Т.к. i²=-1, делаем замену:
(-1)*i-(-1)⁵⁰=-i-1
Задача 2.
1. (17-6i)/(3-4i)=(17-6i)*(3+4i)/(3-4i)*(3+4i)=(51-18i+68i-24i²)/(9-16i²). Т.к. i²=-1, делаем замену:
(51-50i-24*(-1))/(9-16*(-1))=(75+50i)/25
2. (1-i)³= 1³-3*1²*i+3*1*i²-i³=1-3i+3i²-i³. Т.к. i²=-1, делаем замену:
1-3i+3*(-1)-(-1)*i=1-3i-3+i=-2i-2
3. i^40-i^21=(i²)²⁰-i²⁰⁺¹. Т.к. i²=-1, делаем замену:
(-1)²⁰-(-1)²⁰*i=(-1)²⁰*(1-i)=1*(1-i)=1-i
Задача 4.
Пусть х - производительность первого рабочего, у - производительность второго рабочего, тогда 60/х-60/у=3.
За один час оба рабочих производят Х+у деталей.
Составим систему уравнений:
60/х-60/у=3
х+у=30
Первое упростим, из второго уравнения выразим х:
60(х+у)/ху=3 ⇒ 20(х+у)=ху
х=30-у
Подставим в первое уравнение выраженный х, решим уравнение:
20(30-у-у)=у(30-у)
600-40у=30у-у²
у²-70у+600=0
Д-70*70-4*600=2500
у₁=(70-50)/2=10 х₁=30-10=20
у₂=(70+50)/2=60 х₂=30-60=-30 - не удовлетворяет условию
Время , за которое второй рабочий производит 90 деталей: 90/10=9 часов.
ответ: 9 часов
Задача 5.
Пусть х - количество десятков, у - количество единиц. Составим систему уравнений:
у-х=2
(х+у)*(10х+у)=280
Выразим из первого уравнения у и подставим во второе.
у=2+х
(х+2+х)(10х+2+х)=280
Решим получившееся уравнение:
(2х+2)(11х+2)=280
22х²+4х+22х+4=280
22х²+26х-276=0
Д=26²+4*22*276=24964=158²
х₁=(-26+158)/(2*22)=3
х₂=(-26-158)/(2*22) <0 - не удовлетворяет условию
у=2+3=5
Искомое число: 35
ответ: 35
Сравниваем запись в десятичной и двоичной системе.
1111₁₀ = 1*10³ + 1*10² + 1*10¹ + 1*10⁰ = 10000 + 1000 + 100 + 10 + 1
1111₂ = 1*2³ + 1*2² + 1*2¹ + 1*2⁰ = 8 + 4 + 2 + 1 = 15₁₀.
Видим, что для записи двузначного десятичного числа 15 понадобилось четыре разряда в двоичной системе.
Примеры записи чисел: 10₂ = 1*2¹+ 0*2⁰ = 2₁₀ и 100₂ = 1*2² + 0*2¹ + 0*2⁰ = 4₁₀ и
101₂ = 1*2² + 1*2⁰ = 4 + 1 = 5₁₀ и 110₂ = 2² + 2¹ = 4 + 2 = 6₁₀ и 1110₂ = 2³+2²+2¹ = 8 + 4 + 2 = 14₁₀
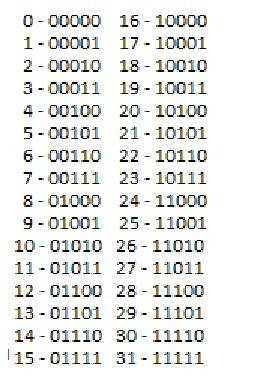
На рисунке в приложении показана запись натуральных чисел от 0 до 31 в двоичной системе исчисления.
В чём же преимущество двоичной системы - в её простоте. В каждом разряде всего два значения - 0 и 1. Недостаток - большое число разрядов для записи числа. Но эту проблему легко решают современные процессоры. Каждый разряд в двоичной системе называется - бит. Число в 32 бит (это 32 единицы в записи) соответствует десятичному числу = 4 294 967 296 , а процессоры в 64 бит могут работать с числами до 1,8*10¹⁹ (19 нулей после запятой). Всего две цифры открывают безграничные возможности.
0,2x-16=24
0,2x-16=-24
x=200
x=-40
x1=-40; x2=200
2)
| 24+0,5x | = 16
24+0,5x=16
24+0,5x=-16
x=-16
x=-80
x1=-80; x2=-16