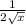= 6x² -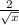 
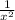
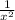)' = (x³)' + (4x²)' - (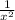)' = 3x² + 8x +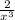 
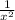)' =(x⁻²)' = -2 * x⁻³ = -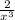 
Пошаговое объяснение:1) f(x)= 2x²-3x+1 , [-1;1] ⇒ f'(x)= 4x-3, найдём критические точки: 4х-3=0, ⇒ х = 3/4=0,75 ∈[-1;1]. Найдём значения функции в критической точке и на концах данного промежутка: f(3/4)= 2·(3/4)²- 3·3/4 +1 =9/8 -9/4 + 1 = -1/8 ; f(1) = 0; f(-1)=6 ⇒ max f(x)=f(-1)=6; minf(x)=f(3/4)=-1/8
2)f(x)=3x²-4 на [2;4] ⇒ f'(x)=6x 6x=0, x=0-крит. точка, но x=0∉ [2;4] ⇒ Найдём значения функции на концах данного промежутка: f(2)= 3·2²-4= 12-4=8 f(4)=3·4² - 4= 48-4=44 ⇒ max f(x)=f(-4)=44; minf(x)=f(2)=8 3)f(x)=x²-1 на [0;3]⇒ f'(x)=2x , 2x=0 x=0 -критическая точка х=0 ∈ [0;3]. Найдём значения функции в критической точке и на концах данного промежутка: f(0) =0²-1=-1; f(3)=3²-1=8 ⇒max f(x)=f(3)=8; minf(x)=f(0)= -1
А что решать то ?Ты хотя бы фотографию сделай...