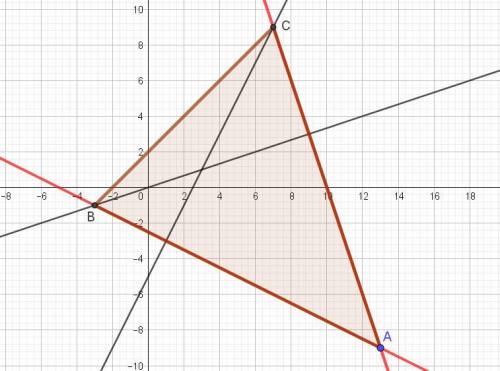
Чтобы узнать, какой вершине треугольника принадлежат координаты точки (13; -9), надо эти координаты подставить в уравнения заданных высот, проведенных из вершин В и С.
При проверке - не подходят, значит, это вершина А.
В уравнениях сторон АВ и АС угловые коэффициенты отрицательно обратны высотам.
АС: у = -3х + в. Подставим координаты точки А:
-9 = -3*13 + в, отсюда в = 39 - 9 = 30.
Получили уравнение стороны АС: у = -3х + 30.
Теперь можно найти координаты точки С, приравняв уравнения АС и высоты к АС: -3х + 30 = 2х - 5, 5х = 35, х = 35/5 = 7, у = -3*7 + 30 = 9.
Точка С(7; 9).
Аналогично определяем координаты точки В( -3; -1).
Відповідь:
а) Окружности касаются друг друга в одной точке.
б) Окружности касаются друг друга в двух точках.
в) Окружности не касаются друг друга
Покрокове пояснення:
Две окружности с центрами удаленными друг от друга на 7 см.
Радиус первой окружности = 3 см.
а) Радиус второй окружности = 4 см.
Сумма радиусов окружностей
3 + 4 = 7 см. - равна расстоянию между окружностями.
Окружности касаются друг друга в одной точке.
б) Радиус второй окружности = 5 см. 5 мм.
Сумма радиусов окружностей
3 + 5,5 = 8,5 см. > 7 см. - больше расстояния между окружностями.
Окружности касаются друг друга в двух точках.
в) Радиус второй окружности = 2 см. 5 мм.
Сумма радиусов окружностей
3 + 2,5 = 5,5 см. < 7 см. - меньше расстояния между окружностями.
Окружности не касаются друг друга.
Так как АС=ВС, то точка F лежит на середине стороны АВ, следовательно BF=AF=225
Тогда АВ=450.
Для чего тогда даны длины других сторон?