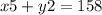
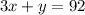
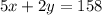
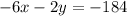
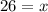
Всего по условию n=15 деталей. Общее число вынуть из ящика пять деталей из 15 будет: n=C(15,5)=15!/5!*(15-5)!=15!/5!*10!=11*12*13*14*15/2*3*4*5=360360/120=3003. Число вынуть пять деталей второго сорта будет C(5,0)*C(10,5). Соответственно четыре детали второго сорта C(5,1)*C(10,4) и три детали второго сорта C(5,2)C(10,3). Общее число споcобов, при которых из пяти деталей вынутыми окажутся хотя бы три детали второго сорта будет: m=C(5,0)*C(10,5)+C(5,1)*C(10,4)+C(5,2)*C(10,3). Тогда общая вероятность вынуть из ящика хотя бы три детали второго сорта будет P=m/n=(C(5,0)*C(10,5)+C(5,1)*C(10,4)+C(5,2)*C(10,3))/C(15,5)=(252+1050+1200)/3003=2502/3003≈0,83.
ответ: 2502/3003≈0,83.
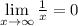
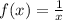является бесконечно малой.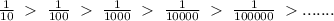
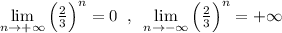
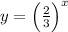убывающая, то при увеличении значений переменной "х" значения функции уменьшаются, стремятся к 0 
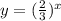является бесконечно малой. 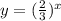является бесконечно большой.
Нехай 92 грн. ми розділяємо на цукерки (3 кг) 60грн , і печиво (1 кг) 32 грн.
Отже 60/3=20 (грн)-коштує 1 кг цукерок
Відповідь : 20 грн коштує килограм цукерок.