966
Пошаговое объяснение:
Пусть всего черных шаров 420x. Тогда всего белых шаров 1.15 * 420x = 483x.
В первой коробке 2/3 всех черных шаров (2/3 * 420x = 280x штук) и 1/7 всех белых шаров (1/7 * 483x = 69x), всего 280x + 69x = 349x шаров.
Во второй коробке оставшиеся шары, их (420 + 483 - 349)x = 554x штук.
Прикинем, какой может быть знаменатель у x (очевидно, x - рациональное число).
69x должно быть целым, так что знаменатель x - делитель 69. 280x - тоже целое, тогда знаменатель x - делитель и 280. Но 69 и 280 взаимно просты, тогда знаменатель у x равен 1, x - целое.
Нужно найти такое целое число, что 349x < 1000 и 554x > 1000.
Второе неравенство в целых числах имеет решением 
, первое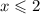 
, так что 
.
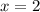Получается, что белых шаров в обеих коробках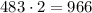 
.
12 = 2*2*3
54 = 2*3*3*3
Надо в итоге добавить в произведение две тройки и одну двойку.
Значит мы m раз умножали на 3, и m-2 раза делили на 3, и всего таких операций было 2m-2 - четное число. И всего операций всех было 60 - тоже четное число
Значит мы четное число раз умножали или делили на 2. Но тогда мы никак не можем изменить число двоек на 1. Мы можем изменить его только на четное число. на 0, на 2, на 4 и так далее.
Мы приходим к противоречию и вынуждены признать, что 54 получить за четное число операций нельзя.
Если на первой трибуне всего 800 мест, а в рядах по 40 мест, то найдем кол-во рядов: 800/40=20 (рядов).
Т.к. кол-во рядов в трибунах одинаково, то и на второй трибуне их 20.
Если на каждом ряду второй трибуны на 5 мест меньше, чем на первой, то их: 40-5=35. И соответственно, общее число мест на второй трибуне: 35*20= 700.
Общее число мест на двух трибунах 800+700=1500