50 ! при каких целых m неравенство |x + 1| + |x − 2| − |x − 3| < m имеет ровно 2017 натуральных решений? если таких m несколько, то в ответе запишите их сумму.
Построим график функции для положительных x. Для этого раскроем модули для разных значений x:
При 0 < x ≤ 2
При 2 < x ≤ 3
При x > 3
Заметим, что при m = 6 имеется 3 натуральных решения. Если увеличить m на 1, то и количество решений возрастёт на 1. Тогда при m = 6 + k число решений будет 3 + k. 2017 = 3 + k ⇒ k = 2014 ⇒ m = 6 + 2014 = 2020.
Общее число кубиков по формуле объема N = 4*5*6 = 120 штук - всего. По три грани окрашено - в вершинах N3= 8 шт По две грани окрашено - на четырёх ребрах без вершин - уменьшаем длину ребра на 2 см каждое. N2= 4*(2+3+4)= 4*9 = 36 штук По одной грани - по 2 грани на 2 см меньше N1 = 2*(2*3+2*4 + 3*4) = 2*(6+8+12) = 52 кубика Совсем не окрашено - внутри кубика - все размеры уменьшаем на 2 см. N0 = 2*3*4 = 24 шт. Проверка: ВСЕГО =8 (по три) + 36 (по две) +52 (по одной) + 24 (не окр.) = 120 шт. ответ: (текст по проверке)
Из жизни дробей. Вы никогда не задумывались, что делают цифры, когда вы закрываете тетрадку? Между прочим, они и без вас неплохо живут! Ходят в гости, складываются и вычитаются, делятся, умножаются… И не всегда на место возвращаются! Ведь не вы же все эти глупые ошибки делаете? Вот однажды две Дроби поссорились. Это не секрет, что у Дробей ужасно скверный характер. То они сокращаться не хотят, то приводиться. Да вы и сами это знаете. На сей раз это были почтенные 17/18 и 18/19. Они выясняли, кто из них больше. (Вы то, конечно, сразу бы определили!) «Я больше!»,- кричит 18/19, -«У меня Числитель больше! Ведь всем известно, что чем больше Числитель, тем больше Дробь!». «Нет!»,- не уступает вторая,- «ты на свой Знаменатель посмотри! У меня Знаменатель меньше, значит, я - больше!». «Да приведитесь вы, наконец, к Общему Знаменателю! Тогда сразу понятно будет»,- советуют им. «Вот еще. Я не желаю иметь с ней ничего общего!»,- не соглашается одна. « Зачем мне эта морока, когда я чувствую, что Я больше», - возражает другая. Пришлось вызывать Уравнителя. А у того есть свой метод, и эталон припасен. Берет ЕДИНИЦУ и отнимает от нее спорщиц. «Так, гражданочки: 1 - (17/18) = 1/18; 1 - (18/19) = 1/19. Выходит-то, что 1/19 МЕНЬШЕ, чем 1/18. Значит, и 18/19 будет немного БЛИЖЕ к ЕДИНИЦЕ, чем 17/18.». А к Уравнителю уж очередь выстроилась ему Решите, кто больше: 92/93 или 93/94? А то ему еще нужно поскорее Обыкновенные Дроби 4/5 и 3/8 в Десятичные перевести, иначе они на самолет опоздают!
Построим график функции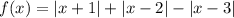
для положительных x. Для этого раскроем модули для разных значений x:
При 0 < x ≤ 2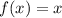
При 2 < x ≤ 3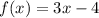
При x > 3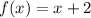
Заметим, что при m = 6 имеется 3 натуральных решения. Если увеличить m на 1, то и количество решений возрастёт на 1. Тогда при m = 6 + k число решений будет 3 + k. 2017 = 3 + k ⇒ k = 2014 ⇒ m = 6 + 2014 = 2020.
ответ: 2020