Пошаговое объяснение:
Задача 5.
Заколдованные весы всегда ошибаются на один и тот же вес в одну и ту же сторону при каждом взвешивании.
Когда взвесили отдельно Артура и отдельно коня, получили вес 19 стоунов и 101 стоун и двойную ошибку
19+101=120 стоунов суммарный вес Артура , коня и двух ошибок.
Когда взвесили Артура на коне получили 114 стоунов и одну ошибку, значит
120-114 = 6 стоунов – это ошибка весов, тогда вес Артура на самом деле будет 19-6= 13 стоунов
ответ : вес Артура 13 стоунов
Задача 6.
Допустим в 1=й клетке сидит 2 кролика.
Тогда во второй клетке сидит тоже 2 кролика.
Значит в 1 клетке по 3 соседа у кролика
Во 2 клетке должно быть у кролика по 7 соседей.
Отсюда в цен тральной клетке 7-3=4 кроликов.
В 4 и 5 клетки по 2 кролика.
И у каждого кролика в центральной клетке будет
3+2+2=7 соседей.
ответ в центральной клетке сидит 4 кролика
Задача 7.
Первый стоит мальчик , значит девочке(№1) , которая стоит за ним надо переместиться на 1 позицию, следующей девочке(№2) надо переместиться на 2 позиции ( поскольку перед ней будет уже 2 мальчика). Следующей №3 на 3 позиции, затем 4..... и последней надо переместиться на 8 позиций. Получаем
1+2+3+4+5+6+7+8= 36
ответ : Было совершено 36 обменов
Задача 8.
Суммы чисел на каждой из пяти линий равны. Значит сумма всех чисел которые используются для заполнения должна делиться на 5. Сложим все числа : 1+2+3+4+5+6+7+8=36.
Не используется либо 1 - (36-1):5=7- делится значит сумма цифр в каждой линии будет (36-1):5*2=14 ( умножаем на 2 поскольку каждое число участвует в 2-х линиях) ,
либо 6 - (36-6):5=5- делится, (36-6):5*2=10 -будет сумма цифр в каждой линии
14 можно получить из суммы 6+8, больше вариантов нет
10 можно получить из суммы 7+3;8+2;6+4:
Так как два ряда содержат 2 цифры, то сумма 14 быть не может( всего один получения суммы), значит Сережа
не использовал цифру 6.
У нас остались цифры 1,2,3,4,5,7,8
Расставим цифры по кружочкам.
Рисунок во вложении
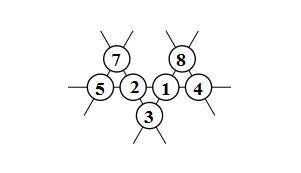
11
Пошаговое объяснение:
В парусном клубе всего 9 джентльменов. Определим количество не повторяющийся пар:
то есть 36 не повторяющийся пар.
Если это не понятно, то можно определить количество не повторяющийся пар следующим образом:
1) c первым джентльменом образуется следующие не повторяющийся пары: {1; 2}, {1; 3}, {1; 4}, {1; 5}, {1; 6}, {1; 7}, {1; 8}, {1; 9}, то есть 8 пар;
2) cо вторым: {2; 3}, {2; 4}, {2; 5}, {2; 6}, {2; 7}, {2; 8}, {2; 9} (пара {2; 1} учтено в паре с первым), то есть 7 пар;
3) c 3: {3; 4}, {3; 5}, {3; 6}, {3; 7}, {3; 8}, {3; 9} (пары {3; 1} и {3; 2} учтены в предыдущих парах, больше об этом не будем повторятся), то есть 6 пар;
4) c 4: {4; 5}, {4; 6}, {4; 7}, {4; 8}, {4; 9}, то есть 5 пар;
5) c 5: {5; 6}, {5; 7}, {5; 8}, {5; 9}, то есть 4 пары;
6) c 6: {6; 7}, {6; 8}, {6; 9}, то есть 3 пары;
7) c 7: {7; 8}, {7; 9}, то есть 2 пары;
8) c 8: {8; 9}, то есть 1 пара.
Тогда получим 1+2+3+4+5+6+7+8=36 не повторяющийся пар.
Теперь определим число наименьшего участия каждой пары. Так как по условию требуется определит наименьшее число кубков, то дадим всем парам равные шансы:
350=9·36+26.
Значит, каждая пара участвовала по 9 раз, и 26 пар участвовали уже 10 раз. Это означает что у всех пар по 9 кубков и у 26 команд дополнительно ещё по кубке.
По условию одна из пар участников заработала больше кубков, чем любая другая. Это означает, что одна из пар схитрила и участвовала не 10 а 11 раз, поэтому у этой пары 11 кубков. Эта пара 12 раз участвовать не может, это опять таки из-за условия "наименьшее число кубков могла добыть".