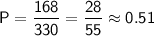Из 11 лотерейных билетов есть 8 выигрышных билетов. Достать 3 выигрышных билетов можно а один не выигрышный билет так как не выигрышных билетов 11-8=3). По правилу произведения , таких вариантов у нас
В связи с очевидной закономерностью возрастания на 3 г. массы каждой следующей гирьки, полный ряд чисел, обозначающих массы гирек, таков: 3 6 9 12 15 18 21 24 27 30 33 36 39 42 45 48 51 54 57 60 63 66 69 Экспериментальным путём можно сначала разложить гирьки на 12 кучек по 69 г. в каждой, а именно так: 66+3=63+6=60+9=57+12=54+15=51+18=48+21=45+24=42+27=39+30=36+33=69 А, как известно, 12 легко делится на 4. 12:4=3 Значит, приравненные выше выражения числа 69 можно разбить на 4 группы (кучки) , соединив по 3 выражения в любой последовательности и комплектации. Общая масса каждой из 4 ёх кучек будет равна 69×3=207 грамм
В связи с очевидной закономерностью возрастания на 3 г. массы каждой следующей гирьки, полный ряд чисел, обозначающих массы гирек, таков: 3 6 9 12 15 18 21 24 27 30 33 36 39 42 45 48 51 54 57 60 63 66 69 Экспериментальным путём можно сначала разложить гирьки на 12 кучек по 69 г. в каждой, а именно так: 66+3=63+6=60+9=57+12=54+15=51+18=48+21=45+24=42+27=39+30=36+33=69 А, как известно, 12 легко делится на 4. 12:4=3 Значит, приравненные выше выражения числа 69 можно разбить на 4 группы (кучки) , соединив по 3 выражения в любой последовательности и комплектации. Общая масса каждой из 4 ёх кучек будет равна 69×3=207 грамм
Из 11 лотерейных билетов есть 8 выигрышных билетов. Достать 3 выигрышных билетов можно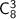
а один не выигрышный билет так как не выигрышных билетов 11-8=3). По правилу произведения , таких вариантов у нас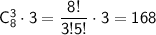 
Количество благоприятных исходов: 168
Количество все возможных исходов: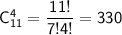
Искомая вероятность: