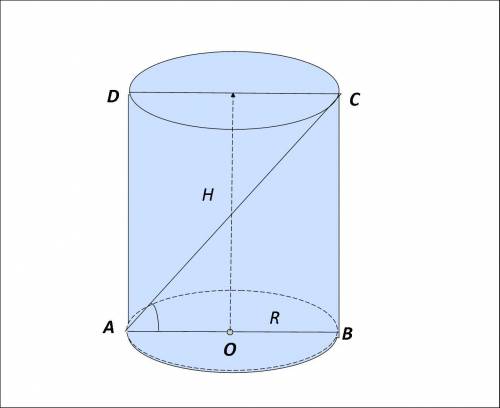
Дано:
цилиндр
ABCD - осевое сечение
АО = ВО = R = 6см
АС - диагональ
∠САВ = 60°
Н - высота цилиндра
Найти: Н
Решение.
Рассмотрим прямоугольный треугольник АВС, в нем:
1) Катет АВ = 2R = 2 · 6см = 12см
2) Если ∠САВ = 60° , тогда ∠АСВ = 30°
3) Катет АВ лежит против угла 30°, значит, гипотенуза АС по величине в 2 раза больше этого катета.
АС = 2АВ
АС = 12см · 2 = 24см
4) По теореме Пифагора найдём катет ВС, который равен высоте цилиндра Н.
ВС² = АС² - АВ²
ВС² = 24² - 12² = 576 - 144 = 432
ВС = √432 = 12√3
Н = ВС = 12√3 см
ответ: 12√3 см
≈ 20,8 см
а^2-b^2+c^2-a^2-c^2+b^2-b^2+c^2=c^2-b^2
-b^2+c^2=C^2-b^2
c^2-b^2=c^2-b^2