Question

Определить сходимость/расходимость ряда (ln n)/n^7. с решением.

Answer 1

$∑_{n=2}^{∞}\frac{㏑(n)}{n^{7}}$.

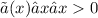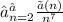Известно, что $㏑(x) ≤ x ∀x 0$, так что $\frac{㏑(n)}{n^{7}} ≤ \frac{n}{n^{7}} = \frac{1}{n^{6}}, так что если [tex]∑_{n=2}^{∞}\frac{1}{n^{6}}$ сходится, то и $∑_{n=2}^{∞}\frac{㏑(n)}{n^{7}}$ сходится.

Ряд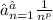 $∑_{n=1}^{∞}\frac{1}{n^{p}}$ сходится, когда p > 1, значит 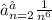$∑_{n=2}^{∞}\frac{1}{n^{6}}$ сходится, отсюда и исходный ряд сходится.

ответ: ряд сходится.