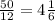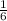Сумма 15 различных натуральных чисел равна 121. найдите наибольшее число.

👇

Ответ:

seniorALFEROV

04.05.2022

По условию задачи, необходимо найти 15 различных натуральных чисел сумма которых равна 121, что на 1 больше, чем сумма первых 15-ти натуральных чисел 1, 2, 3, ..., 15.

Так как число 16 больше числа 15 на 1, то заменяя в последовательности чисел 1, 2, 3, ..., 15 последнее число на 16, мы получим искомый набор 15 различных натуральных чисел.

Наибольшее число в данном наборе 15 различных натуральных чисел — это 16.

ответ: наибольшее число равно 16.

4,8(64 оценок)

Открыть все ответы

Ответ:

1mironov1

04.05.2022

Т.к. на всех этажах по 3 квартиры, то для того,чтобы узнать сколько квартир в подъезде нам нужно кол-во квартир на этаже (3) умножить на кол-во этажей в доме (4). 3*4=12 квартир в 1 подъезде. Глеб живет в 50 квартире, следовательно, мы должны 50/12, получим $\frac{50}{12} = 4 \frac{1}{6}$ , $\frac{1}{6}$ нам "говорит" о том, что это следующий подъезд, 4 подъезда по 12 квартир получается 48, а т.к. Глеб живет в 50 квартире, то это уже сдедующий подъезд, т.е. 5. А т.к. квартир на каждом этаже по 3, то следовательно получаем те 2 квартиры, которые остались находятся на 1 этаже. ответ: Глеб живет в 5 подъезде на 1 этаже

4,8(79 оценок)

Ответ:

brll1bellrf43

04.05.2022

Практическое занятие 2.1.Выражения, уравнения, неравенства.
Среди следующих записей укажите числовые выражения:
а) 42:5;б) 27;в) 32+ -):14;г) 2·7 = 7·2;
д) (17+ 13):10-15;е) 142 > 71·2; ж) 37 – 48+3х
Какие из следующих выражений имеют смысл, если рассматривать их на множестве натуральных чисел:

а) (135+67)· 12;б) (135 - 217):2;в) 362:4?
Какие из нижеприведенных записей являются выражениями с переменными:

а) 8+0,3b; б) 21 - (4 +у); в) х+ 2у< 7; г) 32:у+ 3 = 5у?

Установите, какова область определения выражений, если рассматривать их на множестве действительных чисел:

а) (3 - у) : 64;6) 64 :(3 -у); в) (5 +х) : (х- 12).
Известно, что выражение называется по своему последнему действию. Укажите порядок действий и дайте название каждому выражению:
Выражение
Название выражения
(12·5 + 3:(2+7))·18
(23 - 7·6 - 4+ 15)׃(17-6)
21 + (35·3:8 -14:5)
19 - 8:4 + 5
Выясните, являются ли выражения 3(4 - х) и 12 - 3хтождественно равными на множестве:
а) {1, 2, 3, 4};б) действительных чисел.
Какие из следующих равенств являются тождествами на множестве действительных чисел:
а) 3р + 5m = 5m + 3р; в) 3р · 5m = 5m · 3р;
б) 3р – 5m = 5m - 3р; г) 3р: 5m = 5m:3р?
Обоснуйте каждый шаг в преобразованиях следующих выражений:
а) 324·5 = (300+20+4) · 5 = 300· 5+20·5+4·5 = 500+100+20 = 1500+ 120= 1620;
б) 97·12 = (100 - 3) · 12 = 100 ·12 - 3·12 = 1200 - 36 = 1100+(100 - 36) =1164;
в) 5(1-2х) +10х = 5 - 10х+10х = 5.
Упростите выражение путем тождественных преобразований:
а) 6(2аb- 3) + 2а (6b - 5);б) (12а- 16b):4 - (10а- 4b).
Сравните значения выражений, не выполняя действий:
а) (30 + 56) ·5 и 30·5 + 56·5;
б) (19 + 4) ·7 и 19·7 + 10·7;
в) (14 - 7) ·6 и 16·6 - 7·6;
г) (18 - 9) ·7 и 18·7 - 11·7.
Решите задачу; решение запишите в виде выражения:
На туристическую базу прибыли в один день 150 туристов, на другой день 170. Чтобы пойти по маршрутам, 200 туристов разбились на группы, по 20 человек в каждой, а остальные по 15 человек в группе. Сколько получилось групп?
Среди следующих записей найдите числовые равенства и неравенства:
а) 3х + 4=57:3; б) 34 - 48:12=(7 + 8) ·9; в) 39·3 + 74 - 53; г) 37 < 18; д) 3х + 4< 71; е) 65 > 344 + 148:74
Проверьте, истинны ли числовые равенства:
13 · 93 = 31·39, 14·82 = 41·28, 23·64 = 32·46.
Можно ли утверждать, что произведение любых двух натуральных чисел не изменится, если в каждом множителе переставить цифры?
Известно, что х > у - истинное неравенство. Будут ли истинными следующие неравенства:

а) 2х> 2у; в) 2х- 7 < 2у- 7;

б) < -3 ;г) - 2х - 7 < - 2у- 7?
Известно, что а< b — истинное неравенство. Поставьте вместо * знак «>» или «<» так, чтобы получилось истинное неравенство:

а) -3,7а* -3,7b; б) -* -; в) 0,12а* 0,12b;

г) -2(а + 5) * -2(b + 5); д); е)

Выполните задания, которые предназначаются ученикам начальных классов, и сделайте вывод о том, как трактуются в начальном курсе математики понятия числового равенства и числового неравенства:

а) Запиши два верных равенства и два верных неравенства, используя выражения: 9 ·3, 30 - 6, 3·9, 30 - 3.

б) Расставь скобки так, чтобы равенства были верными: 4 + 2 ·3 = 18; 31- 10 – 3 = 24; 54 – 12 + 8 = 34.

в) Поставь вместо * знаки действий так, чтобы получились верные равенства: 3 * 6 * 2 = 9; 9 * 3 * 6 = 18.
Установите, какие из следующих записей являются уравнениями с одной переменной:

а) (х- 3)·5 = 12х; г) 3 + (12 - 7) ·5 = 16;

б) (х- 3)·5 = 12;д) (х - 3)·у= 12х;

в) (х- 3) - 17 + 12;е) х2 - 2х+ 5 = 0.
Уравнение 2х4+ 4х2- 6 = 0 задано на множестве натуральных чисел. Объясните, почему число 1 является корнем этого уравнения, а 2 и -1 не являются его корнями.
В уравнении (х+ ..)(2х+ 5) - (х- 3)(2х+ 1) = 20 одно число стерто и заменено точками. Найдите стертое число, если известно, что корнем это

4,6(6 оценок)

Это интересно:

Праздники-и-традиции

24.12.2020

Как правильно чистить искуственную елку...

17.04.2022

Как избежать наказания в школе: 10 простых советов...

Образование-и-коммуникации

18.12.2022

Основные принципы подготовки к экзамену без зубрежки...

Здоровье

20.07.2020