Пусть нам дана некоторая прогрессия b(n): b1;b2;b3;b4.
По условию, нам дана сумма каких-то чисел. Давайте запишем их.
Во-первых, у нас дана сумма нечётных членов:
b1 + b3 + b5 + ... + b51 = 28
Во-вторых, сумма членов с чётными номерами равна 7, то есть:
b2 + b4 + b6 + ... + b52 = 7
Запишем эти ряды друг под другом:
b1 + b3 + b5 + ... + b51 = 28
b2 + b4 + b6 + ... + b52 = 7
Теперь каждый член в одном ряду является соседним с соответственным членом в другом ряду.
Замечаем, что знаменателем прогрессии является отношение последующего и предыддущего членов.
q = b2/b1; q = b3/b2 и так далее.
Разделим второй ряд на первый и будем иметь:
b2/b1 + b4/b3 + b6/b5... + b52/b51 = 7/28
Мы знаем, что b2/b1 = q; b4/b3 = q; b52/b51 = q. Всего таких пар 52 / 2 = 26.
То есть, 26q = 7/28.
Отсюда q = 7/28 : 26 = 7/728 = 1/104.
Знаменатель прогрессии равен 1/104
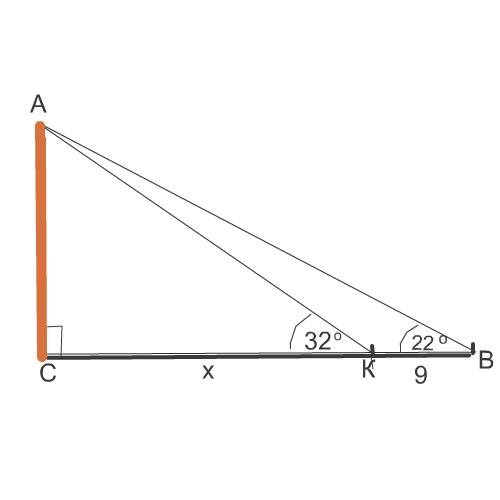
Сделаем простой рисунок.
Обозначим:
вершину дерева А,
его основание С,
вершину угла 32° -К,
вершину угла 22°- В
Пусть расстояние СК от основания С до вершины К угла 32° = х,
тогда расстояние СВ от основания дерева до вершины В угла 22°, удаленной от точки К на 9 метров, = х+9
Высота дерева АС пусть будет =Н
Н:(х+9)=tg(22°) =0.404
Н:х=tg(32°)=0.6249
Н=(х+9)∙tg(22°) =(х+9)*0.404
Н=х∙tg(32°)=х*0.6249
(х+9)∙0.404=х∙0.6∙249
0,404х+3,636=0.6249х
0,2209х=3,636
х=16,4599 м
Н : 16,4599 =0.6249
Н=16,4599∙0.6249=10,2857 м
Высота дерева ≈ 10,286 м
Вот ответ. Вроде бы так, но это не точно