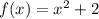 определена на множестве E
определена на множестве E 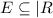
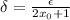 где
где 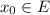 .
. на области
на области 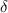 от
от  (то есть:
(то есть: 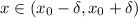 ) выполняется
) выполняется 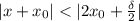 .
.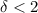 , выполняется
, выполняется 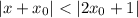 .
.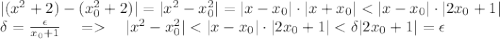
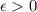 есть
есть 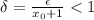 , на области которой выполняется
, на области которой выполняется 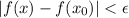
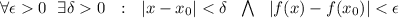 ). Следовательно -
). Следовательно - 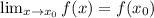 .
.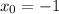 нужно отдельно доказать предел
нужно отдельно доказать предел 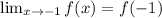 .
. . Но! Множество натуральных чисел
. Но! Множество натуральных чисел 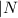 тоже подмножество
тоже подмножество  , значит
, значит 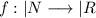 тоже непрерывна, получается - доказали что
тоже непрерывна, получается - доказали что 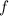 непрерывна на области определения? Известно, что
непрерывна на области определения? Известно, что 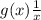 тоже непрерывна на области определения, но
тоже непрерывна на области определения, но 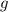 , понятное дело, не определена на
, понятное дело, не определена на  !
! " или, "непрерывна на отрезке
" или, "непрерывна на отрезке 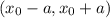 "...
"...Cos²x\2- sin²x\2=sin(π\2-2x) cos²x\2=(1+cosx)\2 sin²x\2=(1-cos)\2 sin(π\2-2x)=cos2x
(1+cosx)\2-(1-cosx)\2=cos2x cos2x=2cos²x-1
1+cosx-1+cosx=2(2cos²x-1)
4cos²x-2cosx-2=0
2cos²x-cosx-1=0 введём замену переменной . Пусть cosx=y
2у²-у-1=0
D=1-4·2·(-1)=9 √D=3
y1=(1+3)\4=1
y2=(1-3)\4=-1\2
Вернёмся к замене : cosx=y1
cosx=1
x=+- arccos1+2πn n∈Z
x=2πn n∈Z
cosx=y2
cosx=-1\2
x=+- arccos(-1\2)+2πm m∈Z
так как значение арккосинуса отрицательное , то arccos(-1\2)=π-π\3=2π\3
x=+-2π\3+2πm m∈Z
Сначала решим правую часть:
0,12-2,5х= -14,7
Теперь перенесем неизвестные (х) в левую часть, а известные - в правую. Если переносим через "равно", то знаки меняем на противоположные.
-2,5х= -14,7-0,12
-2,5х = -14,82
Делим на коэффициент перед переменной:
х = -14,82 / -2,5
х = 5,928
ответ: х=5,928